
【题目】在(2x-3y)10的展开式中,求:
(1)各项的二项式系数的和;
(2)奇数项的二项式系数的和与偶数项的二项式系数的和;
(3)各项系数之和;
(4)奇数项系数的和与偶数项系数的和.
【答案】(1)1024;(2)512 ,512 ;(3)1;(4)见解析
【解析】
(1)根据二项式系数的性质求解;
(2)可采用赋值法,根据二项式定理,求得奇数项的二项式系数的和与偶数项的二项式系数的和,也可直接应用二项式系数的这部分性质,写出答案;
(3)采用赋值法,令x=y=1,求得各项系数之和;
(4)采用赋值法,令x=1,y=-1,结合(3),可分别求得奇数项系数的和与偶数项系数的和.
(1)各项的二项式系数的和为![]() ;
;
(2)奇数项的二项式系数的和为![]()
偶数项的二项式系数的和为![]()
(3)设(2x-3y)10=a0x10+a1x9y+a2x8y2+…+a10y10 (*),各项系数之和即为a0+a1+a2+…+a10,
由于(*)是恒等式,故可用“赋值法”求解.
令(*)中x=y=1,得各项系数之和为(2-3)10=(-1)10=1.
(4)奇数项系数的和为a0+a2+a4+…+a10,偶数项系数的和为a1+a3+a5+…+a9.
由(3)知a0+a1+a2+…+a10=1. ①
令(*)中x=1,y=-1,得a0-a1+a2-a3+…+a10=510. ②
①+②,得2(a0+a2+…+a10)=1+510,故奇数项系数的和为![]() ;
;
①-②,得2(a1+a3+…+a9)=1-510,故偶数项系数的和为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知首项为﹣6的等差数列{an}的前7项和为0,等比数列{bn}满足b3=a7 , |b3﹣b4|=6.
(1)求数列{bn}的通项公式;
(2)是否存在正整数k,使得数列{ ![]() }的前k项和大于
}的前k项和大于 ![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ,求点D的坐标;
,求点D的坐标;
(2)问是否存在实数α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,说明理由.
成立?若存在,求出α,β的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
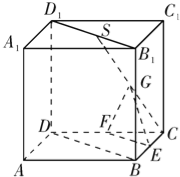
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )

A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设中心在坐标原点,焦点在
中,设中心在坐标原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右准线
,右准线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)已知点![]() 在椭圆
在椭圆![]() 上,求实数
上,求实数![]() 的值;
的值;
(2)已知定点![]() .
.
① 若椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围;
的离心率的取值范围;
② 如图,当![]() 时,记
时,记![]() 为椭圆
为椭圆![]() 上的动点,直线
上的动点,直线![]() 分别与椭圆
分别与椭圆![]() 交于另一点
交于另一点![]() ,若
,若![]() 且
且![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com