Question

解下列不等式；
（1）|x²+3x-8|＞10；（2）5-2x≤

3

x

．

Answer 1

分析：（1）首先将原绝对值不等式转化为二次不等式，再将二次项系数转化为正数，再看二次三项式能否因式分解，若能，则可得方程的两根，且大于号取两边，小于号取中间，若不能，则再“△”，利用求根公式求解方程的根，而后写出解集即可．
（2）将原不等式移项后通分得到

(2x-3)(x-1)

x

≥0，再利用标根结合数轴解此不等式即得．

解答：解：（1）原不等式可化为：
x²+3x-8＞10①或x²+3x-8＜-10②，
解①得：{x|x＜-6或x＞3}；
解②得：{x|-2＜x＜-1}．
故原不等式的解集为：{x|x＜-6或-2＜x＜-1或x＞3}．
（2）原不等式可化为

2x2-5x+3

x

≥0?

(2x-3)(x-1)

x

≥0，
标根如下，

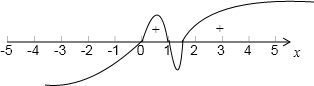
由此可得原不等式的解集为：（0，1]∪[

3

2

，+∞）．

点评：本题考查一元二次不等式的解法、绝对值不等式的解法及分式不等式的解法，是基础题．