
【题目】已知圆锥的顶点为![]() ,底面圆
,底面圆![]() 的两条直径分别为
的两条直径分别为![]() 和
和![]() ,且
,且![]() ,若平面
,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:
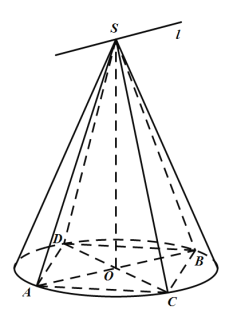
①![]() 平面
平面![]() ;
;
②![]() ;
;
③若![]() 是底面圆周上的动点,则
是底面圆周上的动点,则![]() 的最大面积等于
的最大面积等于![]() 的面积;
的面积;
④![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
其中正确结论的个数是( )
A.1B.2C.3D.4
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点在x轴上,一个顶点为![]() ,离心率为
,离心率为![]() ,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
,过椭圆的右焦点F的直线l与坐标轴不垂直,且交椭圆于A,B两点.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C,B,N三点共线?若存在,求出定点的坐标;若不存在,说明理由;
![]() 设
设![]() ,是线段
,是线段![]() 为坐标原点
为坐标原点![]() 上的一个动点,且
上的一个动点,且![]() ,求m的取值范围.
,求m的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() :
:![]() ,满足
,满足![]() ,则称
,则称![]() 为
为![]() 数列,并记
数列,并记![]() .
.
(1)写出所有满足![]() ,
,![]() 的
的![]() 数列
数列![]() ;
;
(2)若![]() ,
,![]() ,证明:
,证明:![]() 数列是递减数列的充要条件是
数列是递减数列的充要条件是![]() ;
;
(3)对任意给定的正整数![]() ,且
,且![]() ,是否存在
,是否存在![]() 的
的![]() 数列
数列![]() ,使得
,使得![]() ?如果存在,求出正整数
?如果存在,求出正整数![]() 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,以
,以![]() 为直角顶点的等腰直角
为直角顶点的等腰直角![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 均在抛物线
均在抛物线![]() 上.
上.
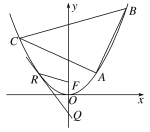
(1)过![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,切点为
,切点为![]() ,点
,点![]() 到切线
到切线![]() 的距离为2,求抛物线
的距离为2,求抛物线![]() 的方程;
的方程;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分别为集合S,T 的元素个数,则下列结论不可能的是( )
A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+m|+|2x-1|.
(1)当m=-1时,求不等式f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出的2人中恰有1人体检3次的概率;
(2)若以这100位会员体检次数的频率分布估计该体检中心所有会员体检次数的概率分布,已知该中心本周共接待了1000名顾客参加体检,试估计该体检中心本周所获利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com