
【题目】已知复数z满足|z|= ![]() ,z2的虚部为2.
,z2的虚部为2.
(1)求z;
(2)设z,z2 , z﹣z2在复平面对应的点分别为A,B,C,求△ABC的面积.
【答案】
(1)解:设Z=x+yi(x,y∈R)
由题意得Z2=(x﹣y)2=x2﹣y2+2xyi
∴ ![]()
故(x﹣y)2=0,∴x=y将其代入(2)得2x2=2∴x=±1
故 ![]() 或
或 ![]()
故Z=1+i或Z=﹣1﹣i;
(2)解:当Z=1+i时,Z2=2i,Z﹣Z2=1﹣i
所以A(1,1),B(0,2),C(1,﹣1)
∴ ![]()
当Z=﹣1﹣i时,Z2=2i,Z﹣Z2=﹣1﹣3i,A(﹣1,﹣1),B(0,2),C(﹣1,﹣3)
S△ABC= ![]() ×1×2=1.
×1×2=1.
【解析】(1)设出复数的代数形式的式子,根据所给的模长和z2的虚部为2.得到关于复数实部和虚部的方程组,解方程组,得到要求的复数.(2)写出所给的三个复数的表示式,根据代数形式的表示式写出复数对应的点的坐标,即得到三角形的三个顶点的坐标,求出三角形的面积,注意三个点的坐标有两种结果,不要漏解.
【考点精析】认真审题,首先需要了解复数的定义(形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部),还要掌握复数的模(绝对值)(复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)
分别叫它的实部和虚部),还要掌握复数的模(绝对值)(复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)![]() (2)
(2)![]() (3)若
(3)若![]() 为虚数,则
为虚数,则![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】如图所示,A,B两点5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P(ξ≥8)= . 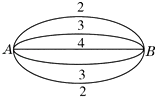
查看答案和解析>>
科目:高中数学 来源: 题型:
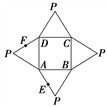
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
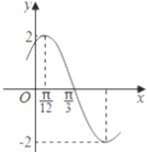
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)将函数![]() 的图象做怎样的平移变换可以得到函数
的图象做怎样的平移变换可以得到函数![]() 的图象;
的图象;
(Ⅲ)若方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证: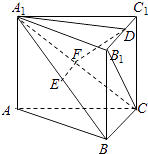
(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
近视度数 | 0﹣100 | 100﹣200 | 200﹣300 | 300﹣400 | 400以上 |
学生频数 | 30 | 40 | 20 | 10 | 0 |
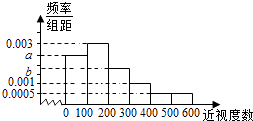
将近视程度由低到高分为4个等级:当近视度数在0﹣100时,称为不近视,记作0;当近视度数在100﹣200时,称为轻度近视,记作1;当近视度数在200﹣400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(1)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(2)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(3)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com