Question

13．设函数f（x）=log_a（2x+1）在区间$（{-\frac{1}{2}，0}）$上满足f（x）＞0．
（1）求实数a的取值范围；
（2）若$f（-\frac{1}{4}）=1$，画出函数g（x）=$\left\{\begin{array}{l}f（x），（x＞-\frac{1}{2}）\\{2^x}，（x≤-\frac{1}{2}）\end{array}$的图象，并解不等式g（x）＜$\frac{1}{2}$．

Answer 1

分析 （1）根据x的取值范围，结合对数函数的图象与性质，求出a的取值范围；
（2）根据题意求出a的值，再画出函数g（x）的图象，结合图形把不等式g（x）＜$\frac{1}{2}$化为对数或指数不等式，从而求出不等式的解集．

解答 解：（1）∵x∈$（{-\frac{1}{2}，0}）$，∴2x∈（-1，0），
∴2x+1∈（0，1），
又f（x）＞0，
∴实数a的取值范围是0＜a＜1； …（4分）
（2）由$f（-\frac{1}{4}）=1$，得log_a（2×（-$\frac{1}{4}$）+1）=1，
解得$a=\frac{1}{2}$，…（5分）
所以g（x）=$\left\{\begin{array}{l}{{log}_{\frac{1}{2}}（2x+1），x＞-\frac{1}{2}}\\{{2}^{x}，x≤-\frac{1}{2}}\end{array}\right.$，…（6分）
画出函数的图象，如图所示：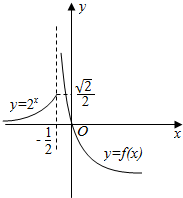

…（9分）
当$x＞-\frac{1}{2}$时，不等式g（x）＜$\frac{1}{2}$可化为
${log_{\frac{1}{2}}}（2x+1）＜\frac{1}{2}$，即$2x+1＞\frac{{\sqrt{2}}}{2}$，
解得$x＞\frac{{\sqrt{2}}}{4}-\frac{1}{2}$；…（10分）
当$x≤-\frac{1}{2}$时，不等式g（x）＜$\frac{1}{2}$可化为
${2^x}＜\frac{1}{2}$，
解得 x＜-1；…（11分）
综上，不等式的解集为$（-∞，-1）∪（\frac{{\sqrt{2}}}{4}-\frac{1}{2}，+∞）$．…（12分）

点评 本题考查了指数、对数函数的图象与性质的应用问题，也考查了分段函数的应用问题，是综合性题目．