分析:(I)由题设知|OA|=8
,BC边和y轴的夹角为30°,设B(x,y),则x=|OB|sin30°=4
,y=|OB|cos30°=12,由B(4
,12)在x
2=2py上,知
(4)2=2p×12,由此能求出抛物线方程.
(II)由(I)知A(-4
,12),B(4
,12),且y=
x2,所以
y′=x,由导数的几何意义能求出直线l
1,l
2的方程以及这两条直线的交点坐标.
解答:解:(I)∵等边三角形OAB的边长为
8(点O为坐标原点),
且三个顶点均在抛物线E:x
2=2py(p>0)上,
∴|OA|=8
,BC边和y轴的夹角为30°,
设B(x,y),则x=|OB|sin30°=4
,y=|OB|cos30°=12,
∵B(4
,12)在x
2=2py上,∴
(4)2=2p×12,
∴p=2.
∴抛物线方程为x
2=4y.
(II)由(I)知A(-4
,12),B(4
,12),且y=
x2,
∴
y′=x,
∴k
A=
×(-4)=-2
,
∴直线l
1的方程为y-12=-2
(x+4
),即2
x+y+12=0.
kB=×4=2
,
∴直线l
2的方程为y-12=2
(x-4
),即2
x-y-12=0.
解方程组
,得x=0,y=-12.
∴直线l
1,l
2的交点坐标为(0,-12).
点评:本题考查抛物线方程的求法,解题时要认真审题,仔细解答,注意导数的几何意义的合理运用.



 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案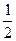 (O为坐标原点).
(O为坐标原点). 轴不垂直时,
轴不垂直时, 点C,使得△ABC为等边三角形,求a
点C,使得△ABC为等边三角形,求a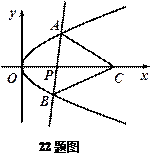
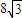 (点O为坐标原点),且三个顶点均在抛物线E:x2=2py(p>0)上.
(点O为坐标原点),且三个顶点均在抛物线E:x2=2py(p>0)上.