
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 是椭圆
是椭圆![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ![]() ,且离心率为
,且离心率为![]() .设
.设![]() 为椭圆
为椭圆![]() 的左、右顶点,P为椭圆上异于
的左、右顶点,P为椭圆上异于![]() 的一点,直线
的一点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,且直线
两点,且直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求证:直线![]() 与
与![]() 的斜率之积为定值;
的斜率之积为定值;
(Ⅲ)判断三点![]() 是否共线,并证明你的结论.
是否共线,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: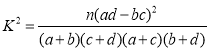 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.

(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com