
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.

科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间![]() (单位:天)的函数,且销售量满足
(单位:天)的函数,且销售量满足![]() =
=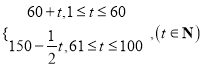 ,价格满足
,价格满足![]() =
=![]() .
.
(1)求该种商品的日销售额![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点. 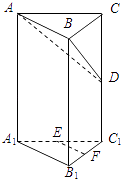
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x).当x∈[0,1]时,f(x)=2x.若在区间[﹣2,3]上方程ax+2a﹣f(x)=0恰有四个不相等的实数根,则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2)
,2)
D.(1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com