
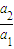 可得公比q,从而可判断
可得公比q,从而可判断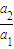 可得公比q,故能确定数列是该数列的“基本量”①对;
可得公比q,故能确定数列是该数列的“基本量”①对;

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①S1与S2;②a2与S3;③a1与an;④q与an.其中n为大于1的整数,Sn为{an}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
①S1与S2;②a2与S3;③a1与an;④q与an中,一定能成为该数列“基本量”的是第_____________.其中n为大于1的整数,Sn为{an}的前n项和.
查看答案和解析>>
科目:高中数学 来源:河北省唐山一中2010高考模拟试卷(四)(理) 题型:填空题
若干个能唯一确定一个数列的量称为该数列的“基本量”,设{ }是公比为q的无穷等比数列,下列{
}是公比为q的无穷等比数列,下列{ }的四组量中,一定能成为该数列的“基本量”的是第 组。(写出所有符合要求的组号)
}的四组量中,一定能成为该数列的“基本量”的是第 组。(写出所有符合要求的组号)
① 与
与 ②
② 与
与 ③
③ 与
与 ④q与
④q与
其中n为大于1的整数, 为{
为{ }前n项和。
}前n项和。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com