Question

【题目】已知
（1）求的值；
（2）当x∈（﹣t，t]（其中t∈（﹣1，1），且t为常数）时，f（x）是否存在最小值，如果存在求出最小值；如果不存在，请说明理由；
（3）当f（x﹣2）+f（4﹣3x）≥0时，求满足不等式f（x﹣2）+f（4﹣3x）≥0的x的范围．

Answer 1

【答案】解：（1）令，解得﹣1＜x＜1，即函数f（x）的定义域为（﹣1，1），关于原点对称．
又f（﹣x）=loga=loga()-1=﹣loga=﹣f（x），
所以f（x）为奇函数，
所以=﹣=0．
（2）设﹣1＜x1＜x2＜1，
则﹣=．
因为﹣1＜x1＜x2＜1，
所以﹣＞0，即＞．
所以在（﹣1，1）上为减函数，也在（﹣t，t]上为减函数，
①当a＞1时，y=logat单调递增，t=单调递减，所以y=loga在（﹣t，t]上单调递减，
此时f（x）存在最小值为f（t）=log．
②当0＜a＜1时，y=logat单调递减，t=单调递减，所以y=loga在（﹣t，t]上单调递增，
此时f（x）不存在最小值．
综①②知，当a＞1时，f（x）存在最小值为f（t）=loga．
（3）f（x﹣2）+f（4﹣3x）≥0可化为f（x﹣2）≥﹣f（4﹣3x），
由（1）知f（x）为奇函数，所以f（x﹣2）≥f（3x﹣4），
①当a＞1时，由（2）知f（x）在（﹣1，1）上为减函数，
所以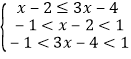，解得1＜x＜．
②当0＜a＜1时，由（2）知f（x）在（﹣1，1）上为增函数，
所以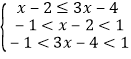，解得为．
综①②得满足不等式f（x﹣2）+f（4﹣3x）≥0的x的范围为：（1，）．
【解析】（1）由所求表达式的特点知，可判断函数的奇偶性；
（2）根据复合函数单调性的判定方法判断f（x）的单调性，由单调性可讨论f（x）的最小值情况；
（3）利用f（x）的奇偶性把f（x﹣2）+f（4﹣3x）≥0可化为f（x﹣2）≥f（3x﹣4），再利用f（x）的单调性即可解出不等式．
【考点精析】本题主要考查了函数单调性的性质和函数的值的相关知识点，需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法才能正确解答此题．