
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求实数
上单调递增,求实数![]() 的值;
的值;
(2)是否存在实数![]() ,使得
,使得![]() 在
在![]() 上单调递减,若存在,试求
上单调递减,若存在,试求![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若![]() ,当
,当![]() 时不等式
时不等式![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求导函数,根据函数f(x)在(-![]() ,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;(2)由题意得:f′(x)=3x2+2ax-2≤0在(-2,
,1)上单调递减,在(1,+∞)上单调递增,可得x=1是方程f′(x)=0的根,从而可求实数a的值;(2)由题意得:f′(x)=3x2+2ax-2≤0在(-2, ![]() )上恒成立,由此可实数a的取值范围;(3)求导函数,求导函数x∈(-1,2)时,f(x)的最小值,欲使不等式f(x)<m有解,只需m≥[f(x)]min,从而可求实数m的取值范围.
)上恒成立,由此可实数a的取值范围;(3)求导函数,求导函数x∈(-1,2)时,f(x)的最小值,欲使不等式f(x)<m有解,只需m≥[f(x)]min,从而可求实数m的取值范围.
试题解析:
(1)![]() ,
,
∵![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 是方程
是方程![]() 的根,解得
的根,解得![]()
(2)由题意得: ![]() 在
在![]() 上恒成立,
上恒成立,
∴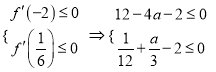 ∴
∴![]()
(3)当![]() 时,
时, ![]() ,
,
由![]() 得:
得: ![]()
列表:
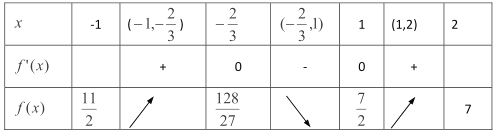
∴![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,此时
,此时![]() ,
,
欲使![]() 有解,只需
有解,只需![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4个男生,3个女生站成一排.(必须写出算式再算出结果才得分)
(Ⅰ)3个女生必须排在一起,有多少种不同的排法?
(Ⅱ)任何两个女生彼此不相邻,有多少种不同的排法?
(Ⅲ)甲乙二人之间恰好有三个人,有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最值;
上的最值;
(3)当![]() 时,对大于1的任意正整数
时,对大于1的任意正整数![]() ,试比较
,试比较![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“鸡兔同笼”问题是我国古代著名的趣题之一.《孙子算经》中就记载了这个有趣的问题.书中这样描述:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔几何?
试设计一个算法,输入鸡兔的总数量和鸡兔的脚的总数量,分别输出鸡、兔的数量,写出程序语句.并画出相应的程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.

(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
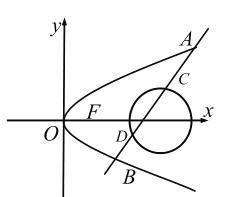
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com