
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某县农民年均收入服从μ=500元,σ=20元的正态分布,求:
(1)此县农民的年均收入在500~520元之间的人数的百分比;
(2)此县农民的年均收入超过540元的人数的百分比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a<﹣1,函数f(x)=|x3﹣1|+x3+ax(x∈R).
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)已知存在实数m,n(m<n≤1),对任意t0∈(m,n),总存在两个不同的t1 , t2∈(1,+∞),
使得f(t0)﹣2=f(t1)=f(t2),求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,如图.
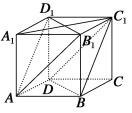
(1)求证:平面AB1D1∥平面C1BD;
(2)试找出体对角线A1C与平面AB1D1和平面C1BD的交点E,F,并证明:A1E=EF=FC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某批次同一型号的产品共10件,其中有8件合格品,2件次品.
(Ⅰ)某检验员从中有放回地连续抽取产品2次,每次随机抽取1件,求两次都取到次品的概率;
(Ⅱ)若该检验员从中任意抽取2件,用X表示取出的2件产品中次品的件数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
, ![]() )的图象关于直线
)的图象关于直线![]() 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为![]() .
.
(1)求函数![]() 的解析式以及它的单调递增区间;
的解析式以及它的单调递增区间;
(2)是否存在实数![]() ,满足不等式
,满足不等式 ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=![]() a,
a,
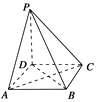
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com