
【题目】已知直线l: ![]() ,曲线C:
,曲线C: 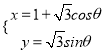
(1)当m=3时,判断直线l与曲线C的位置关系;
(2)若曲线C上存在到直线l的距离等于![]() 的点,求实数m的范围.
的点,求实数m的范围.
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() 相交于
相交于![]() ,
, ![]() ,点
,点![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 的周长为16,
的周长为16, ![]() 的周长为12.
的周长为12.
(1)求椭圆![]() 的标准方程与离心率;
的标准方程与离心率;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的一般方程.
的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足Sn=2n+1+2p(n∈N*).
(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足![]() =(3+p)anbn,求数列{bn}的前n项和Tn.
=(3+p)anbn,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: 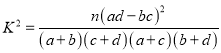
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A. ①② B. ②③
C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,a10=4a3,a4=3a1+7.
(1)求通项公式an;
(2)若bn=an-2an+2,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com