
【题目】已知f(x)=sinx﹣cosx,x∈[0,+∞).
(1)证明: ![]() ;
;
(2)证明:当a≥1时,f(x)≤eax﹣2.
【答案】
(1)解:不等式 ![]() ,即不等式
,即不等式 ![]() ,
,
设 ![]() ,则g'(x)=﹣sinx+x,x∈[0,+∞),
,则g'(x)=﹣sinx+x,x∈[0,+∞),
再次构造函数h(x)=﹣sinx+x,则h'(x)=﹣cosx+1≥0在x∈[0,+∞)时恒成立,
所以函数h(x)在[0,+∞)上单调递增,
所以h(x)≥h(0)=0,
所以g'(x)≥0在[0,+∞)上恒成立,
所以函数g(x)在[0,+∞)上单调递增,
所以g(x)≥g(0)=0,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() 成立
成立
(2)解:由(1)的解析可知,当x∈[0,+∞)时,sinx≤x且 ![]() ,
,
所以 ![]() ,
,
当 ![]() 对x∈[0,+∞)恒成立时,不等式f(x)≤eax﹣2恒成立,
对x∈[0,+∞)恒成立时,不等式f(x)≤eax﹣2恒成立,
不等式 ![]() ,即不等式
,即不等式 ![]() ,对x∈[0,+∞)恒成立,
,对x∈[0,+∞)恒成立,
构造函数 ![]() ,
,
则M'(x)=ex﹣x﹣1,
令m(x)=ex﹣x﹣1,
则m'(x)=ex﹣1,当x∈[0,+∞)时,m'(x)≥0,
故m(x)在[0,+∞)上单调递增,
所以m(x)≥m(0)=0,故M'(x)≥0,即M(x)在[0,+∞)上单调递增,
所以M(x)≥M(0)=0,
故 ![]() 恒成立,
恒成立,
故当a≥1时, ![]() ,
,
即当a≥1时,不等式f(x)≤eax﹣2恒成立
【解析】(1)设 ![]() ,则g'(x)=﹣sinx+x,x∈[0,+∞),再次构造函数h(x)=﹣sinx+x,则h'(x)=﹣cosx+1≥0在x∈[0,+∞)时恒成立,可得g'(x)≥0在[0,+∞)上恒成立,可得
,则g'(x)=﹣sinx+x,x∈[0,+∞),再次构造函数h(x)=﹣sinx+x,则h'(x)=﹣cosx+1≥0在x∈[0,+∞)时恒成立,可得g'(x)≥0在[0,+∞)上恒成立,可得 ![]() ,即可得证.(2)由(1)可知,不等式
,即可得证.(2)由(1)可知,不等式 ![]() ,对x∈[0,+∞)恒成立,构造函数
,对x∈[0,+∞)恒成立,构造函数 ![]() ,令m(x)=ex﹣x﹣1,则m'(x)=ex﹣1,当x∈[0,+∞)时,m'(x)≥0,可得
,令m(x)=ex﹣x﹣1,则m'(x)=ex﹣1,当x∈[0,+∞)时,m'(x)≥0,可得 ![]() 恒成立,从而得证,当a≥1时,不等式f(x)≤eax﹣2恒成立.
恒成立,从而得证,当a≥1时,不等式f(x)≤eax﹣2恒成立.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)为偶函数,且满足f(x)=f(x+2),f(﹣1)=1,若数列{an}的前n项和Sn满足2Sn=an+1 , a1= ![]() ,则f(a5)+f(a6)=( )
,则f(a5)+f(a6)=( )
A.4
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=2BC=2CD=2,△SAD为正三角形.
(Ⅰ)点M为棱AB上一点,若BC∥平面SDM,AM=λAB,求实数λ的值;
(Ⅱ)若BC⊥SD,求二面角A-SB-C的余弦值.

【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由线面平行的性质定理可得![]() ,据此可知四边形BCDM为平行四边形,据此可得
,据此可知四边形BCDM为平行四边形,据此可得![]() .
.
(Ⅱ)由几何关系,在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立空间坐标系,据此可得平面
,以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立空间坐标系,据此可得平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,据此计算可得二面角
,据此计算可得二面角![]() 余弦值为
余弦值为![]() .
.
(Ⅰ)因为![]() 平面SDM,
平面SDM,![]()
![]() 平面ABCD,平面SDM
平面ABCD,平面SDM ![]() 平面ABCD=DM,所以
平面ABCD=DM,所以![]() ,
,
因为![]() ,所以四边形BCDM为平行四边形,又
,所以四边形BCDM为平行四边形,又![]() ,所以M为AB的中点.
,所以M为AB的中点.
因为![]()
![]() .
.

(Ⅱ)因为![]()
![]() ,
, ![]()
![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
又由题知![]() ,所以
,所以![]() 所以
所以![]() ,
,
以下建系求解.以点E为坐标原点,EA方向为X轴,EC方向为Y轴,ES方向为Z轴建立如图所示空间坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则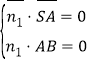 ,所
,所![]() ,
,
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
同理得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
 ,因为二面角
,因为二面角![]() 为钝角.
为钝角.
所以二面角![]() 余弦值为
余弦值为![]() .
.
【点睛】
本题考查了立体几何中的判断定理和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,明确角的构成.同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(Ⅰ)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(Ⅱ)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在(![]() ,
,![]() ](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:
](n=1,2,3,4,5)时,日平均派送量为50+2n单.若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由。
(参考数据:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax,a>0.
(1)记f(x)的极小值为g(a),求g(a)的最大值;
(2)若对任意实数x恒有f(x)≥0,求f(a)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某路段最高限速60km/h,电子监控测得连续6辆汽车的速度用茎叶图表示如下(单位:km/h).若从中任取2辆,则恰好有1辆汽车超速的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂生产某种产品的过程中记录的几组数据,其中![]() 表示产量(单位:吨),
表示产量(单位:吨),![]() 表示生产中消耗的煤的数量(单位:吨).
表示生产中消耗的煤的数量(单位:吨).
|
|
|
|
|
|
|
|
|
|
|
|
(1)试在给出的坐标系下作出散点图,根据散点图判断,在![]() 与
与![]() 中,哪一个方程更适合作为变量
中,哪一个方程更适合作为变量![]() 关于
关于![]() 的回归方程模型?(给出判断即可,不需要说明理由)
的回归方程模型?(给出判断即可,不需要说明理由)
(2)根据(1)的结果以及表中数据,建立变量![]() 关于
关于![]() 的回归方程.并估计生产
的回归方程.并估计生产![]() 吨产品需要准备多少吨煤.参考公式:
吨产品需要准备多少吨煤.参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com