
【题目】已知![]() .
.
(1)当![]() 时,不等式
时,不等式![]() 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)求证:当![]() 时,
时,![]() .
.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)依题意,当x≥0时,![]() 恒成立.
恒成立.
设![]() ,则x≥0时,k(x)≥0恒成立,
,则x≥0时,k(x)≥0恒成立,
若![]() ,则x>0时,
,则x>0时,![]() ,k(x)在[0,+∞)上为增函数.
,k(x)在[0,+∞)上为增函数.
于是,x≥0时,k(x)≥k(0)=0.因此,![]() 符合要求.
符合要求.
若![]() ,则2m>1,0<x<ln(2m)时,k'(x)<0,k(x)在
,则2m>1,0<x<ln(2m)时,k'(x)<0,k(x)在![]() 上为减函数.
上为减函数.
于是,![]() .因此,
.因此,![]() 不符合要求.
不符合要求.
所以m的取值范围为![]() .
.
(2)解法一:设![]() ,则
,则![]() .
.
当x<ln4时,g'(x)<0;当x>ln4时,g'(x)>0
所以g(x)在(-∞,ln4]上为减函数,在[ln4,+∞)上为增函数.
所以g(x)≥g(ln4)=4-4ln4.
由此可得,g(x)=ex-4x≥4-4ln4,即![]() ,
,
当且仅当x=ln4时等号成立.
所以x>0时,![]()
![]() ,
,
当且仅当x=ln4时等号成立.
设h(x)=4x-4lnx-4,则![]() .
.
当0<x<1时,h'(x)<0;当x>1时,h'(x)>0.
所以h(x)在(0,1]上为减函数,在[1,+∞)上为增函数.
所以h(x)≥h(1)=0,即![]() ,
,
当且仅当x=1时等号成立.故![]() .
.
由于上述两个等号不同时成立,因此![]() .
.
所以当x>0时,f(x)>4lnx+8-8ln2.
解法二:设![]() ,
,
则![]() .
.
由g"(x)=![]() ,知g'(x)为增函数.
,知g'(x)为增函数.
又g'(1)=e-4<0,g'(2)=e2-2>0,因此,g'(x)有唯一零点,设为x0.
则x0∈(1,2),且0<x<x0时,g'(x)<0;x>x0时,g'(x)>0
所以g(x)在区间(0,x0]上为减函数,在区间[x0,+∞)上为增函数.
所以g(x)有最小值![]() .
.
又由![]() ,知
,知![]() ,
,
两边取对数,得![]() .
.
所以![]()
 .
.
所以当x>0时,g(x)≥g(x0)>0,故当x>0时,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的长轴长为
的长轴长为![]() ,点
,点![]() 、
、![]() 、
、![]() 为椭圆上的三个点,
为椭圆上的三个点,![]() 为椭圆的右端点,
为椭圆的右端点,![]() 过中心
过中心![]() ,且
,且![]() ,
,![]() .
.

(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 是椭圆上位于直线
是椭圆上位于直线![]() 同侧的两个动点(异于
同侧的两个动点(异于![]() 、
、![]() ),且满足
),且满足![]() ,试讨论直线
,试讨论直线![]() 与直线
与直线![]() 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左右焦点分别为![]() ,
,![]() 的椭圆的离心率为
的椭圆的离心率为![]() ,焦距为
,焦距为![]() ,A,B是椭圆上两点.
,A,B是椭圆上两点.
(1)若直线![]() 与以原点为圆心的圆相切,且
与以原点为圆心的圆相切,且![]() ,求此圆的方程;
,求此圆的方程;
(2)动点P满足:![]() ,直线
,直线![]() 与
与![]() 的斜率的乘积为
的斜率的乘积为![]() ,求动点P的轨迹方程.
,求动点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,![]() ,点M是SA的中点,
,点M是SA的中点,![]() ,
,![]() ,
,![]() .
.
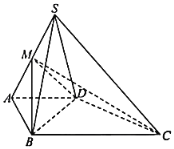
(1)求证:![]() 平面SCD;
平面SCD;
(2)若直线SD与底面ABCD所成的角为![]() ,求平面MBD与平面SBC所成的锐二面角的余弦值.
,求平面MBD与平面SBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
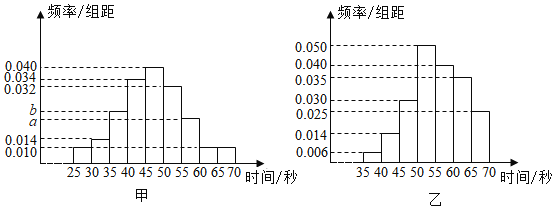
(1)若甲解开密码锁所需时间的中位数为47,求a、b的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①求该团队能进入下一关的概率;
②该团队以怎样的先后顺序派出人员,可使所需派出的人员数目X的数学期望达到最小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,且
是边长为2的正方形,且![]() ,若点E,F分别为AB和CD的中点.
,若点E,F分别为AB和CD的中点.
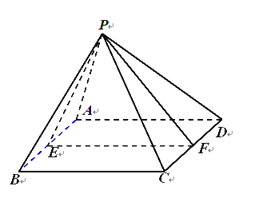
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成![]() 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
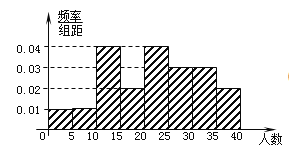
A.  B.
B. 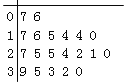
C. 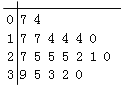 D.
D. 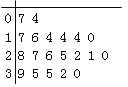
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com