
【题目】已知函数f(x)=![]() ,其中a为常数.
,其中a为常数.
(1)当a=1时,求f(x)的最大值;
(2)若f(x)在区间(0,e]上的最大值为-2,求a的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用导数分析单调性,进而求最值;
(2)利用分类讨论![]() ,
,![]() 时函数f(x)的单调性与此时的最大值,并由已知构建方程求得参数即可.
时函数f(x)的单调性与此时的最大值,并由已知构建方程求得参数即可.
(1)易知f(x)的定义域为(0,+∞),当a=1时,f(x)=-x+ln x,f′(x)=-1+![]() =
=![]() ,
,
令f′(x)=0,得x=1.当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
∴f(x)max=f(1)=-1.
∴当a=-1时,函数f(x)在(0,+∞)上的最大值为-1.
(2)f′(x)=![]() -a
-a![]() ,x∈(0,e],
,x∈(0,e],![]() ∈
∈![]() .
.
①若![]() ,则f′(x)≥0,从而f(x)在(0,e]上是增函数,
,则f′(x)≥0,从而f(x)在(0,e]上是增函数,
∴f(x)max=f(e)=![]() ≥0,不合题意.
≥0,不合题意.
②若![]() ,令f′(x)>0得
,令f′(x)>0得![]() -a >0,结合x∈(0,e],解得0<x<
-a >0,结合x∈(0,e],解得0<x<![]() ;
;
令f′(x)<0得![]() -a <0,结合x∈(0,e],解得
-a <0,结合x∈(0,e],解得![]() <x≤e.
<x≤e.
从而f(x)在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
∴f(x)max=![]() =
=![]() -1=
-1=![]() ,
,
得![]() ,即a=
,即a=![]() .
.
∵![]()
![]() ,∴a=
,∴a=![]() 为所求.
为所求.
故实数a的值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 分别是
分别是![]()
![]()
![]() 的中点.
的中点.
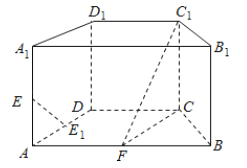
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与面
与面![]() 所成角的大小;
所成角的大小;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织甲、乙、丙、丁、戊、己等6名学生参加演讲比赛,采用抽签法决定演讲顺序,在“学生甲和乙都不是第一个出场,且甲不是最后一个出场”的前提下,学生丙第一个出场的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种排列,在欧洲这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中出现了如图所示的表,这是我国数学史上的一次伟大成就,如图所示,在“杨辉三角”中去除所有为1的项,依次构成数列,2,3,3,4,6,4,5 ,10 ,10,5,……,则此数列的前119项的和为__________.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有男生27名,女生18名,用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.
(1)求从该班男生、女生中分别抽取的人数;
(2)为协助敬老院做好卫生清扫工作,从参加活动的5名学生中随机抽取2名,求这2名学生均为女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C的中心在原点,抛物线![]() 的焦点是双曲线C的一个焦点,且双曲线过点
的焦点是双曲线C的一个焦点,且双曲线过点![]() .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线![]() 与双曲线C交于A,B两点,试问:k为何值时,
与双曲线C交于A,B两点,试问:k为何值时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() .若满射
.若满射![]() ,满足:对任意的
,满足:对任意的![]() ,
,![]() ,则称
,则称![]() 为“和谐函数”.记
为“和谐函数”.记 ![]() ,
,![]() .设“和谐映射”
.设“和谐映射”![]() 为满足条件:存在正整数
为满足条件:存在正整数![]() ,使得(1)当
,使得(1)当![]() 时,若
时,若![]() ,
,![]() ,则
,则![]()
![]()
![]() ;(2)若
;(2)若![]() ,
,![]() ,则
,则![]() ,求
,求![]() 的最大可能值.
的最大可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com