
【题目】已知数列{an}中,a1=1,an>0,前n项和为Sn,若![]() (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)记![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【答案】(1) an=2n﹣1;(2) Tn![]() .
.
【解析】
(1)根据题意,有an=Sn﹣Sn﹣1,结合![]() 分析可得
分析可得![]() 1,则数列{
1,则数列{![]() }是以
}是以![]() 1为首项,公差为1的等差数列,由等差数列的通项公式可得
1为首项,公差为1的等差数列,由等差数列的通项公式可得![]() 1+(n﹣1)=n,则Sn=n2,据此分析可得答案;
1+(n﹣1)=n,则Sn=n2,据此分析可得答案;
(2)由(1)的结论可得cn=(2n﹣1)×22n﹣1;进而可得Tn=1×2+3×23+5×25+……+(2n﹣1)×22n﹣1,由错位相减法分析可得答案.
(1)数列{an}中,an=Sn﹣Sn﹣1,(n∈N*,且n≥2)①
![]() ,(n∈N*,且n≥2)②
,(n∈N*,且n≥2)②
①÷②可得:![]() 1,
1,
则数列{![]() }是以
}是以![]() 1为首项,公差为1的等差数列,
1为首项,公差为1的等差数列,
则![]() 1+(n﹣1)=n,
1+(n﹣1)=n,
则Sn=n2,
当n=1时,a1=S1=1,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣1,
a1=1也符合该式,
则an=2n﹣1;
(2)有(1)的结论,an=2n﹣1,
则cn=(2n﹣1)×22n﹣1;
则Tn=1×2+3×23+5×25+……+(2n﹣1)×22n﹣1,③;
则4Tn=1×23+3×25+5×27+……+(2n﹣1)×22n+1,④;
③﹣④可得:﹣3Tn=2+2(23+25+……+22n﹣1)﹣(2n﹣1)×22n+1![]() (
(![]() 2n)×22n+1,
2n)×22n+1,
变形可得:Tn![]() .
.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,其离心率
的左、右焦点,其离心率![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
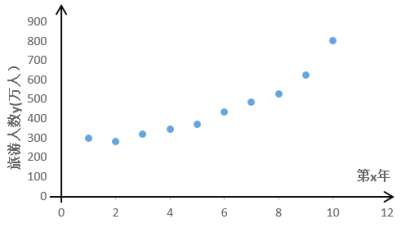
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为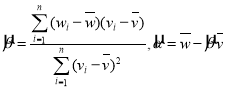 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数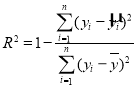 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]()
![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上的点到直线l的最大距离为
上的点到直线l的最大距离为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校教务处对学生学习的情况进行调研,其中一项是:对“学习数学”的态度是否与性别有关,可见随机抽取了30名学生进行了问卷调查,得到了如下联表:
男生 | 女生 | 合计 | |
喜欢 | 10 | ||
不喜欢 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人,抽到喜欢“学习数学”的学生的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程);
(2)若从喜欢“学习数学”的女生中抽取2人进行调研,其中女生甲被抽到的概率为多少?(要写求解过程)
(3)试判断是否有95%的把握认为喜欢“学习数学”与性别有关?
附: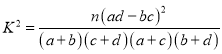 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识,高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人,女生200人;文科班有男生100人,女生300人.现按男、女用分层抽样从理科生中抽取6人,按男、女分层抽样从文科生中抽取4人,组成环境保护兴趣小组,再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.
(1)设事件![]() 为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件
为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示抽取的4人中文科女生的人数,求
表示抽取的4人中文科女生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为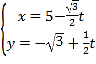 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com