
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 不重合),交
不重合),交![]() 轴于
轴于![]() 点. 圆
点. 圆![]() 过
过![]() 三点.下列说法正确的是( )
三点.下列说法正确的是( )
① 圆心![]() 在直线
在直线![]() 上;
上;
② ![]() 的取值范围是
的取值范围是![]() ;
;
③ 圆![]() 半径的最小值为
半径的最小值为![]() ;
;
④ 存在定点![]() ,使得圆
,使得圆![]() 恒过点
恒过点![]() .
.
A. ①②③B. ①③④C. ②③D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在xOy平面上,将双曲线的一支![]()
![]() 及其渐近线
及其渐近线![]() 和直线
和直线![]() 、
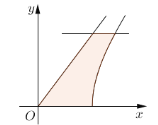
、![]() 围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周所得的几何体为
围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周所得的几何体为![]() ,过
,过![]()
![]() 作
作![]() 的水平截面,计算截面面积,利用祖暅原理得出
的水平截面,计算截面面积,利用祖暅原理得出![]() 体积为________
体积为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1 , x2 , 当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1 , y2 , 使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.
则 ① , ②
, ② ,
,
③ , ④
, ④![]() ,
,
四个函数中为不严格增函数的是 ,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售量8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com