
| π |
| 2 |
| oz1 |
| oz1 |
| 3 |
| 4 |
| oz2 |
| oz2 |
| A、+12tgθ-1 | ||
B、
| ||
C、
| ||
D、
|
| 5 |
| 4 |
| 5 |
| 4 |
| cosθ |
| 2sinθ |
| π |
| 2 |
| (2 sinθ)2+cos2θ |
| 1+3sin2θ |
| 1+3sin2θ |
| 2sinθ | ||
|
| cosθ | ||
|
| 1+3sin2θ |
| 2sinθ | ||
|
| cosθ | ||
|
| cosθ |
| 2sinθ |
| 1+3sin2θ |
| 3π |
| 4 |
| 3π |
| 4 |
| 1+3sin2θ |
| 3π |
| 4 |
| 3π |
| 4 |
| 1+3sin2θ |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| sin∅ |
| cos∅ |
sin(
| ||
cos(
|
| 5π |
| 4 |
| π |
| 4 |
| 1+tanβ |
| 1-tanβ |
1+
| ||
1-
|
| 2sinθ+cosθ |
| 2sinθ-cosθ |
| 2tanθ+1 |
| 2tanθ-1 |


科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 2 |
| OZ1 |
| OZ1 |
| 3π |
| 4 |
| OZ2 |
| OZ2 |
查看答案和解析>>
科目:高中数学 来源: 题型:013
设复数z1=2sinθ+icosθ(![]() <θ<
<θ<![]()
![]() 在复平面上对应向量
在复平面上对应向量![]() ,将
,将![]() 按顺时针方向旋转
按顺时针方向旋转![]() π后得到向量
π后得到向量![]() ,
,![]() 对应的复数为z2=
对应的复数为z2=
r(cos![]() +isin
+isin![]() ),则tan
),则tan![]() 等于(
)
等于(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
r(cos![]() +isin
+isin![]() ),则tan
),则tan![]() 等于(
)
等于(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学第三轮复习精编模拟试卷08(理科)(解析版) 题型:解答题
 <θ<
<θ<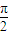 )在复平面上对应向量
)在复平面上对应向量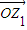 ,将
,将 按顺时针方向旋转
按顺时针方向旋转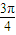 后得到向量
后得到向量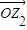 ,
,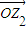 对应的复数为z2=r(cosφ+isinφ),则tanφ= .
对应的复数为z2=r(cosφ+isinφ),则tanφ= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com