
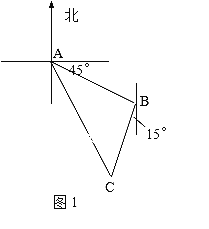
【题目】如图1,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,应沿什么方向,用多少h能尽快追上乙船?
科目:高中数学 来源: 题型:
【题目】设a、b、c成等比数列,非零实数x,y分别是a与b,b与c的等差中项.
(1)已知 ①a=1、b=2、c=4,试计算 ![]() 的值;
的值;
②a=﹣1、b= ![]() 、c=﹣
、c=﹣ ![]() ,试计算
,试计算 ![]() 的值
的值
(2)试推测 ![]() 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省2017届高中毕业年级考前预测数学(理)】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015江苏高考,18】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
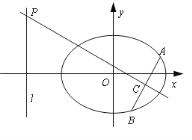
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于
cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于 ![]()
(1)求ω的取值范围及函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ![]() ,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com