
【题目】已知命题p:在△ABC中,若AB<BC,则sinC<sinA;命题q:已知a∈R,则“a>1”是“ ![]() <1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
<1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
A.1
B.2
C.3
D.4
【答案】A
【解析】解:命题p:在△ABC中,若AB<BC,则sinC<sinA;根据正弦定理得到命题p是真命题;
命题q:已知a∈R,则“a>1”是“ ![]() <1”的必要不充分条件;由a>1
<1”的必要不充分条件;由a>1 ![]() ;
; ![]() 推不出a>1,因为a可能小于0;故命题q是假命题;
推不出a>1,因为a可能小于0;故命题q是假命题;
所以命题p∧q是假命题,p∨q是真命题,(¬p)∨q是假命题,(¬p)∧q是假命题,
故在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为1个;
故选:A.
【考点精析】本题主要考查了复合命题的真假的相关知识点,需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. 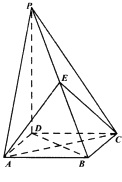
(1)求证:平面AEC⊥平面PDB;
(2)当PD=2AB,且E为PB的中点,求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,将
,将![]() 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)可近似看作一次函数
(元/件)可近似看作一次函数![]() 的关系(如图所示).
的关系(如图所示).

(1)由图象,求函数![]() 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价﹣成本总价)为![]() 元.试用销售单价
元.试用销售单价![]() 表示毛利润
表示毛利润![]() ,并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
,并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是()
①若直线![]() 与直线
与直线![]() 平行,则直线
平行,则直线![]() 平行于经过直线
平行于经过直线![]() 的所有平面;②平行于同一个平面的两条直线互相平行;③若
的所有平面;②平行于同一个平面的两条直线互相平行;③若![]() 是两条直线,
是两条直线,![]() 是两个平面,且
是两个平面,且![]() ,
,![]() ,则
,则![]() 是异面直线;④若直线恒过定点(1,0),则直线方程可设为
是异面直线;④若直线恒过定点(1,0),则直线方程可设为![]() .
.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcos(x+ ![]() )+
)+ ![]() .
.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在区间[0, ![]() ]上的最大值及最小值.
]上的最大值及最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com