
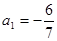 ,
,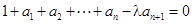 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),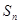 为数列{an}的前
为数列{an}的前 项和.
项和.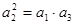 ,求
,求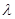 的值;
的值;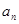 ;
;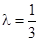 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由. ;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。
;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。 ,得到
,得到 ,令
,令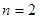 ,得到
,得到 。…………2分
。…………2分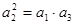 ,计算得
,计算得 .……………………………………………………4分
.……………………………………………………4分 ,可得:
,可得: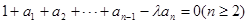 ,所以有
,所以有
 ,又
,又 ,……………………5分
,……………………5分 ,故数列
,故数列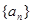 从第二项起是等比数列。……………7分
从第二项起是等比数列。……………7分 ,所以n≥2时,
,所以n≥2时, ……………………………8分
……………………………8分 …………………………………10分
…………………………………10分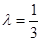 所以
所以 ……………………………………11分
……………………………………11分 )´4k–2 =
)´4k–2 =  ´4m–2 +
´4m–2 +  ´4p–2,化简得:2´4k - p= 4m–p+1
´4p–2,化简得:2´4k - p= 4m–p+1 )´4p–2 = –
)´4p–2 = – + (
+ ( )´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
)´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:不详 题型:单选题
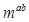 <1,则m的取值范围是( )
<1,则m的取值范围是( )| A.m>1 | B.1<m<8 |
| C.m>8 | D.0<m<1或m>8 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中,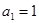 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有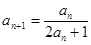 .
. 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式; 的前n项和为
的前n项和为 ,求使得
,求使得 的最小正整数
的最小正整数 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 为第三项,9为第六项的等比数列的公比,则这个三角形是
为第三项,9为第六项的等比数列的公比,则这个三角形是| A.钝角三角形 | B.锐角三角形 | C.等腰直角三角形 | D.以上都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
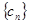 满足
满足 ,
,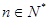 ,数列
,数列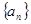 满足
满足
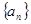 的通项公式;(5分)
的通项公式;(5分)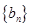 满足
满足 ,
, 为数列
为数列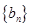 的前
的前 项和.求
项和.求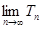 ;(5分)
;(5分) ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有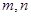 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com