【题目】已知函数
（
）.
（1）若
，讨论
的单调性；
（2）若在区间
内有两个极值点，求实数a的取值范围.
【答案】（1）
在
上单调递减，在
上单调递增. （2）
【解析】
（1）求出函数的导数，解关于导函数的方程，求出函数的单调区间，求出函数的极值即可；
（2）求出函数的导数，通过讨论
的范围，求出函数的单调区间，结合函数的零点个数确定的范围即可．
解：（1）由题意可得的定义域为
，
当
时，易知
∴由
得
，由
得
，
∴在上单调递减，在上单调递增.
（2）由（1）可得
，
当时，
，
记
，则
，
∵在内有两个极值点，
∴
在内有两个零点，
∴
.
令
，则
，
当
，即
时，
，所以在上单调递减，
的图像至多与x轴有一个交点，不满足题意.
当
，即
时，在上
，单调递增，
的图像至多与x轴有一个交点，不满足题意.
当
，即
时，在
上单调递增，在
上单调递减
由
知，要使在内有两个零点，必须满足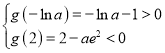
，解得
.
综上，实数a的取值范围是.
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案科目：高中数学 来源： 题型：
【题目】(2017·衢州调研)已知四棱锥P－ABCD的底面ABCD是菱形，∠ADC＝120°，AD的中点M是顶点P在底面ABCD的射影，N是PC的中点.
(1)求证：平面MPB⊥平面PBC；
(2)若MP＝MC，求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
．证明：
（1）存在唯一x0∈（0,1），使f(x0)＝0；
（2）存在唯一x1∈（1，2），使g(x1)＝0，且对(1)中的x0，有x0＋x1<2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,直线l的参数方程为
(t为参数,
).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,直线l的倾斜角
,P点坐标为
,求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】生男生女都一样，女儿也是传后人.由于某些地区仍然存在封建传统思想，头胎的男女情况可能会影响生二孩的意愿，现随机抽取某地200户家庭进行调查统计.这200户家庭中，头胎为女孩的频率为0.5，生二孩的频率为0.525，其中头胎生女孩且生二孩的家庭数为60.
（1）完成下列
列联表，并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关；
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
（2）在抽取的200户家庭的样本中，按照分层抽样的方法在头胎生女孩家庭中抽取了5户，进一步了解情况，在抽取的5户中再随机抽取3户，求这3户中恰好有2户生二孩的概率.
附：
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
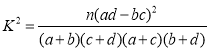（其中
）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱
中，
平面
，
，
，且
，
，
分别为棱
，
，
的中点.
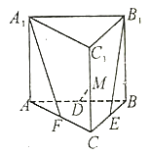
（1）证明：直线
与
共面；并求其所成角的余弦值；
（2）在棱
上是否存在点
，使得
平面
，若存在，求
的值；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
