
【题目】已知函数f(x)![]() 是R上的奇函数.
是R上的奇函数.
(1)求a,b的值;
(2)判断并证明f(x)的单调性;
(3)若对任意实数x,不等式f[f(x)﹣m]![]() 0恒成立,求m的取值范围.
0恒成立,求m的取值范围.
【答案】(1)a=1,b=1,(2)单调递增,见解析(3)(﹣∞,2].
【解析】
(1)由奇函数的定义求解,![]() 求得
求得![]() ,再由
,再由![]() 求得
求得![]() ,再验证此时
,再验证此时
符合题意.
(2)由单调性定义证明;
(3)先计算出函数值![]() ,因此由单调性得f(x)﹣m>﹣3,即m<f(x)+3=4
,因此由单调性得f(x)﹣m>﹣3,即m<f(x)+3=4![]() ,于是求出4
,于是求出4![]() 的最小值或取值范围即可.
的最小值或取值范围即可.
(1)∵f(x)![]() 是R上的奇函数,
是R上的奇函数,
∴f(0)=0,即![]() ,
,
所以,a=1,
又f(﹣1)+f(1)=0,
所以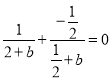 ,
,
∴b=1,此时![]() 是奇函数;
是奇函数;
(2)由(1)可得f(x)![]() 1
1![]() ,
,
设x1![]() x2,则
x2,则![]() .
.
则f(x1)﹣f(x2)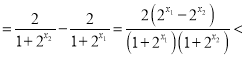 0,
0,
∴f(x1)![]() f(x2),
f(x2),
故f(x)在R上单调递增,
(3)对任意实数x,不等式f[f(x)﹣m]![]() 0恒成立,
0恒成立,
∴不等式f[f(x)﹣m]![]() 恒成立,且f(﹣3)
恒成立,且f(﹣3)![]() ,
,
由(2)可知f(x)在R上单调递增,
∴f(x)﹣m![]() ﹣3,即m
﹣3,即m![]() f(x)+3=4
f(x)+3=4![]() ,
,
结合指数函数的性质可知,![]() ,
,
∴2<4![]() 4,
4,
∴m≤2,
故m的范围(﹣∞,2].


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() ,有下列说法:
,有下列说法:
(1)函数![]() 满足
满足![]() 则函数在
则函数在![]() 上不是单调减函数;
上不是单调减函数;
(2)对任意的![]() 函数
函数![]() 满足
满足![]() 则函数在
则函数在![]() 上是单调增函数;
上是单调增函数;
(3)函数![]() 满足
满足![]() 则函数
则函数![]() 是偶函数;
是偶函数;
(4)函数![]() 满足
满足![]() 则函数
则函数![]() 不是奇函数.
不是奇函数.
其中,正确的说法是________(填写相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每公斤![]() 元,成本为每公斤
元,成本为每公斤![]() 元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失
元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失![]() 元.根据以往的销售情况,按
元.根据以往的销售情况,按![]() ,
,![]() ,
,![]() ,
,![]() ,
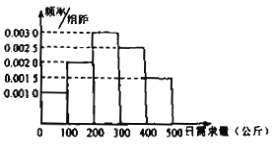
,![]() 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
(1)根据频率分布直方图计算该种鲜鱼日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了![]() 公斤这种鲜鱼,假设当天的需求量为
公斤这种鲜鱼,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于
不小于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD>BC.E,F分别为棱AB,PC上的点.

(1)求证:平面AFD⊥平面PAB;
(2)若点E满足![]() ,当F满足什么条件时,EF∥平面PAD?请给出证明.
,当F满足什么条件时,EF∥平面PAD?请给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ,经统计,其高度均在区间
,经统计,其高度均在区间![]() ,
,![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.

(1)求图中![]() 的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且a1=![]() ,an+1=Sn+
,an+1=Sn+![]() (n∈N*,t为常数).
(n∈N*,t为常数).
(Ⅰ)若数列{an}为等比数列,求t的值;
(Ⅱ)若t>﹣4,bn=lgan+1,数列{bn}前n项和为Tn,当且仅当n=6时Tn取最小值,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线![]() 至少经过其样本数据
至少经过其样本数据![]() 中的一个点
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
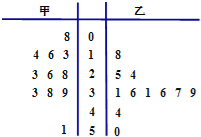
A. X乙﹣X甲=5,甲比乙得分稳定
B. X乙﹣X甲=5,乙比甲得分稳定
C. X乙﹣X甲=10,甲比乙得分稳定
D. X乙﹣X甲=10,乙比甲得分稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com