Question

【题目】连接正方体每个面的中心构成一个正八面体，则该八面体的外接球与内切球体积之比为______．

Answer 1

【答案】.

【解析】

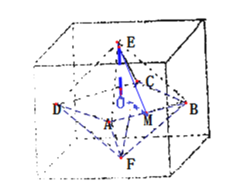
正八面体中ABCD四点或AFCE四点所组成的截面在外接球的一个大圆面上，可得其对角线的长度即为外接球的直径，又正方体中心设为O，取AB中点M，则在直角△OME中，斜边ME上的高即为内切球的半径，由此能求出结果．

若正八面体的外接球的各个顶点都在同一个球面上，

则其中ABCD四点或AFCE四点所组成的截面在球的一个大圆面上，

可得，此四点组成的正方形是球的大圆的一个内接正方形，

其对角线的长度即为球的直径，

设正八面体边长为2，且每个侧面三角形均为等边三角形，

故FE=AC=2，则外接球的半径是，

又正方体中心设为O，取AB中点M，则在直角△OME中，斜边ME==，

斜边ME上的高即为内切球的半径，大小为=，

∴外接球与内切球半径之比为，∴外接球与内切球体积之比为

故答案为．