若定义在R上的函数f(x)对任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-1成立,且当x>0时,f(x)>1.
(1)求证:f(x)-1为奇函数;
(2)求证:f(x)是R上的增函数;
(3)若f(4)=5,解不等式f(3m2-m-2)<3.
分析:(1)要判断函数的奇偶性方法是f(x)+f(-x)=0.现在要判断f(x)-1的奇偶性即就是判断[f(x)-1]+[f(-x)-1]是否等于0.首先令x1=x2=0得到f(0)=1;然后令x1=x,x2=-x,则f(x-x)=f(x)+f(-x)-1证出即可;
(2)要判断函数的增减性,就是在自变量范围中任意取两个x1<x2∈R,判断出f(x1)与f(x2)的大小即可知道增减性.
(3)已知f(x1+x2)=f(x1)+f(x2)-1,且f(4)=5,则f(4)=f(2)+f(2)-1?f(2)=3.由不等式
f(3m2-m-2)<3,得f(3m2-m-2)<f(2),由(2)知,f(x)是R上的增函数,得到3m2-m-2<2,求出解集即可.
解答:解:(1)定义在R上的函数f(x)对任意的x
1,x
2∈R,都有f(x
1+x
2)=f(x
1)+f(x
2)-1成立,
令x
1=x
2=0,则f(0+0)=f(0)+f(0)-1?f(0)=1,
令x
1=x,x
2=-x,则f(x-x)=f(x)+f(-x)-1,
∴[f(x)-1]+[f(-x)-1]=0,
∴f(x)-1为奇函数.
(2)由(1)知,f(x)-1为奇函数,
∴f(-x)-1=-[f(x)-1],
任取x
1,x
2∈R,且x
1<x
2,则x
2-x
1>0,
∵f(x
1+x
2)=f(x
1)+f(x
2)-1,
∴f(x
2-x
1)=f(x
2)+f(-x
1)-1=f(x
2)-[f(x
1)-1]=
f(x
2)-f(x
1)+1.
∵当x>0时,f(x)>1,
∴f(x
2-x
1)=f(x
2)-f(x
1)+1>1,∴f(x
1)<f(x
2),
∴f(x)是R上的增函数.
(3)∵f(x
1+x
2)=f(x
1)+f(x
2)-1,且f(4)=5,
∴f(4)=f(2)+f(2)-1?f(2)=3.
由不等式f(3m
2-m-2)<3,得f(3m
2-m-2)<f(2),
由(2)知,f(x)是R上的增函数,
∴3m
2-m-2<2,∴3m
2-m-4<0,∴-1<m<
,
∴不等式f(3m
2-m-2)<3的解集为(-1,
).
点评:考查学生掌握判断函数奇偶性能力和判断函数增减性的能力,灵活运用题中已知条件的能力.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案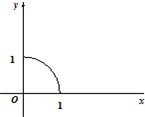 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为( )
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为( )