
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
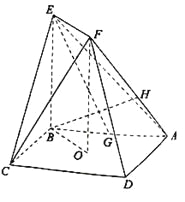
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角OEFC的正弦值;
(Ⅲ)设H为线段AF上的点,且AH=![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
试题(Ⅰ)利用空间向量证明线面平行,关键是求出平面的法向量,利用法向量与直线方向向量垂直进行论证;(Ⅱ)利用空间向量求二面角,关键是求出平面的法向量,再利用向量数量积求出法向量夹角,最后根据向量夹角与二面角相等或互补关系求正弦值;(Ⅲ)利用空间向量求线面角,关键是求出平面的法向量,再利用向量数量积求出向量夹角,最后根据向量夹角与线面角互余关系求正弦值.
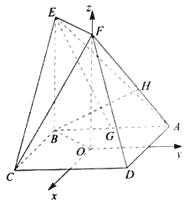
试题解析:依题意,![]() ,如图,以
,如图,以![]() 为点,分别以
为点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系,依题意可得
轴的正方向建立空间直角坐标系,依题意可得![]() ,
,![]() .
.
(Ⅰ)证明:依题意,![]() .
.
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则 ,即
,即![]() .
.
不妨设![]() ,可得
,可得![]() ,又
,又![]() ,可得
,可得![]() ,
,
又因为直线![]() ,所以
,所以![]() .
.
(Ⅱ)解:易证,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
依题意,![]() .
.
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则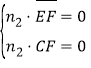 ,即
,即![]() .
.
不妨设![]() ,可得
,可得![]() .
.
因此有 ,于是
,于是![]() ,
,
所以,二面角![]() 的正弦值为
的正弦值为![]() .
.
(Ⅲ)解:由![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() ,进而有
,进而有![]() ,从而
,从而![]() ,因此
,因此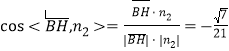 .
.
所以,直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲乙两人进行跳棋比赛,约定每局胜者得1分,负者得0分.若其中的一方比对方多得2分或下满5局时停止比赛.设甲在每局中获胜的概率为![]() ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为![]() ,且各局胜负相互独立.
,且各局胜负相互独立.
(1)求没下满5局甲就获胜的概率;
(2)设比赛结束时已下局数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价![]() (元)与销量
(元)与销量![]() (万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)
(万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)

(Ⅰ)求售价15元时的销量及此时的供货价格;
(Ⅱ)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() ,
,![]() :
:![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个![]() 单位长度,得到曲线
单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:

已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.

参考公式:![]() ,其中
,其中 ![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数图象的有下列说法:
①若函数![]() 满足
满足![]() ,则
,则![]() 的一个周期为
的一个周期为![]() ;
;
②若函数![]() 满足
满足![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若函数![]() 与函数
与函数![]() 的图象关于原点对称,则
的图象关于原点对称,则![]() ,
,
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的图象关于直线
的图象关于直线![]() 对称,则正确的选项是( )
对称,则正确的选项是( )
①.函数![]() 为奇函数
为奇函数
②.函数![]() 在
在![]() 上单调递增
上单调递增
③.若![]() ,则
,则![]() 的最小值为
的最小值为![]()
④.函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象
的图象
A.①③B.①④C.①②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
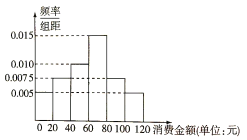
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
),![]() .
.
(1)求证:![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com