
【题目】如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:
①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;
④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.
其中正确的是 (写出所有正确命题的编号).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,圆
,圆![]() 与直线
与直线![]() 相切,
相切,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 任作一直线
任作一直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,记
两点,记![]() ,若在线段
,若在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,试判断当直线
,试判断当直线![]() 运动时,点
运动时,点![]() 是否在某一定直一上运动?若是,请求出该定直线的方程;若不是,请说明理由.
是否在某一定直一上运动?若是,请求出该定直线的方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,第五组
,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
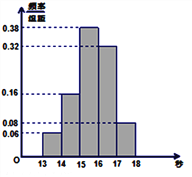
(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,当
,当![]() (
(![]() 是自然对数底数)时,函数
是自然对数底数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为![]() 的等边
的等边![]() 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)设![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(2)如果![]() 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,![]() 的位置应在哪里?如果
的位置应在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 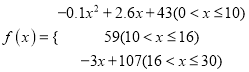 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com