
【题目】以下四个命题:①设![]() ,则
,则![]() 是
是![]() 的充要条件;②已知命题
的充要条件;②已知命题![]() 、
、![]() 、
、![]() 满足“
满足“![]() 或
或![]() ”真,“
”真,“![]() 或
或![]() ”也真,则“
”也真,则“![]() 或
或![]() ”假;③若
”假;③若![]() ,则使得
,则使得![]() 恒成立的
恒成立的![]() 的取值范围为{
的取值范围为{![]() 或
或![]() };④将边长为
};④将边长为![]() 的正方形
的正方形![]() 沿对角线
沿对角线![]() 折起,使得
折起,使得![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() .其中真命题的序号为________.
.其中真命题的序号为________.
【答案】①③④
【解析】
①中,根据对数函数的运算性质,即可判定;②中,根据复合命题的真假判定方法,即可判定;③中,令![]() ,转化为
,转化为![]() 在
在![]() 恒成立,即可求解;④中,根据几何体的结构特征和椎体的体积公式,即可求解.
恒成立,即可求解;④中,根据几何体的结构特征和椎体的体积公式,即可求解.
由题意,①中,当![]() ,根据对数函数的运算性质,可得
,根据对数函数的运算性质,可得![]() ,
,
反证,当![]() 时,可得
时,可得![]() ,所以“
,所以“![]() ”是“
”是“![]() ”成立的充要条件,所以是正确的;
”成立的充要条件,所以是正确的;
②中,若命题““![]() 或
或![]() ”真”,可得命题
”真”,可得命题![]() 中至少有一个是真命题,当
中至少有一个是真命题,当![]() 为真命题,则
为真命题,则![]() 假命题,此时若“
假命题,此时若“![]() 或
或![]() ”真,则命题
”真,则命题![]() 为真命题,所以“
为真命题,所以“![]() 或
或![]() ”真命题,所以不正确;
”真命题,所以不正确;
③中,令![]() ,则不等式
,则不等式![]() 恒成立转化为
恒成立转化为![]() 在
在![]() 恒成立,
恒成立,
则满足![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,所以是正确的;
,所以是正确的;
④中,如图所示,O为AC的中点,连接DO,BO,
则![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,
其中![]() 也是等腰直角三角形,
也是等腰直角三角形,![]() 平面
平面![]() ,
,
![]() 为三棱锥
为三棱锥![]() 的高,且
的高,且![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]() ,所以是正确的,
,所以是正确的,
综上可知真命题的序号为①③④



科目:高中数学 来源: 题型:
【题目】下列五个命题:
①“![]() ”是“
”是“![]() 为R上的增函数”的充分不必要条件;
为R上的增函数”的充分不必要条件;
②函数![]() 有两个零点;
有两个零点;
③集合![]() ,
,![]() ,从A,B中各任意取一个数,则这两数之和等于4的概率是
,从A,B中各任意取一个数,则这两数之和等于4的概率是![]() ;
;
④动圆C既与定圆![]() 相外切,又与y轴相切,则圆心C的轨迹方程是
相外切,又与y轴相切,则圆心C的轨迹方程是![]() ;
;
⑤若对任意的正数x,不等式![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() .
.
其中正确的命题序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将红、黑、蓝、白5张纸牌(其中白纸牌有2张)随机分发给甲、乙、丙、丁4个人,每人至少分得1张,则下列两个事件为互斥事件的是( )
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中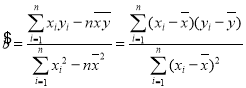 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点.
中点.
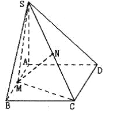
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求实数
,求实数![]() 的值,使得直线
的值,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
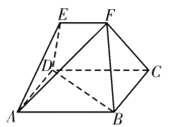
(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,![]() ⊥底面
⊥底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

(1)求证:![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);
(3)若直线![]()
![]() 与平面
与平面![]() 所成角分别为
所成角分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com