
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作互相垂直的两条直线分别与
作互相垂直的两条直线分别与![]() 相交于
相交于![]() ,
,![]() 和
和![]() ,
,![]() 四点.
四点.
(1)四边形![]() 能否成为平行四边形,请说明理由;
能否成为平行四边形,请说明理由;
(2)求![]() 的最小值.
的最小值.
【答案】(1)见解析.
(2)![]() .
.
【解析】
试题分析:(1)若四边形![]() 为平行四边形,则四边形
为平行四边形,则四边形![]() 为菱形, ∴
为菱形, ∴![]() 与
与![]() 在点
在点![]() 处互相平分,又
处互相平分,又![]() 的坐标为
的坐标为![]() 显然这时
显然这时![]() 不是平行四边形.
不是平行四边形.
(2)直线![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,消去
,与椭圆方程联立,消去![]() ,利用韦达定理及弦长公式
,利用韦达定理及弦长公式![]() ,
,
令![]() ,则
,则![]() .考虑当直线
.考虑当直线![]() 的斜率不存在时和直线
的斜率不存在时和直线![]() 的斜率为零时情况得到
的斜率为零时情况得到![]() 的最小值
的最小值
试题解析:设点![]()
(Ⅰ)若四边形![]() 为平行四边形,则四边形
为平行四边形,则四边形![]() 为菱形,
为菱形,
∴![]() 与
与![]() 在点
在点![]() 处互相平分,又F的坐标为
处互相平分,又F的坐标为![]() ,由椭圆的对称性知
,由椭圆的对称性知![]() 垂直于
垂直于![]() 轴,则
轴,则![]() 垂直于
垂直于![]() 轴,
轴,
显然这时![]() 不是平行四边形.
不是平行四边形.
∴四边形![]() 不可能成为平行四边形.
不可能成为平行四边形.
(Ⅱ) 当直线![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]()
由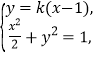 消去
消去![]() 得,
得,![]()
∴![]()
∴![]() 同理得,
同理得,![]() .∴
.∴![]() ,
,
令![]() ,则
,则![]() .
.
当直线![]() 的斜率不存在时,则
的斜率不存在时,则![]()
当直线![]() 的斜率为零时,则
的斜率为零时,则![]()
![]() ,∴
,∴![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某届世界杯足球赛上,a,b,c,d四支球队进入了最后的比赛,在第一轮的两场比赛中,a对b,c对d,然后这两场比赛的胜者将进入冠亚军决赛,这两场比赛的负者比赛,决出第三名和第四名.比赛的一种最终可能结果记为acbd(表示a胜b,c胜d,然后a胜c,b胜d).
(1)写出比赛所有可能结果构成的样本空间;
(2)设事件A表示a队获得冠军,写出A包含的所有可能结果;
(3)设事件B表示a队进入冠亚军决赛,写出B包含的所有可能结果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计![]() 的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对
的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对![]() ;②若卡片上的
;②若卡片上的![]() 能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为
能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为![]() ;④根据统计数
;④根据统计数![]() 估计
估计![]() 的值.假如本次试验的统计结果是
的值.假如本次试验的统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值约为( )
的值约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:对于任意的实数
满足:对于任意的实数![]() 都有
都有![]() 成立,且当
成立,且当![]() 时,
时, ![]() 恒成立,且
恒成立,且![]() 是一个给定的正整数).
是一个给定的正整数).
(1)判断函数![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)判断并证明![]() 的单调性;若函数
的单调性;若函数![]() 在
在![]() 上总有
上总有![]() 成立,试确定
成立,试确定![]() 应满足的条件;
应满足的条件;
(3)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设有5个条件类似的女孩(把她们分别记为A,B,C,D, E)应聘秘书工作,但只有2个秘书职位,因此5个人中只有2人能被录用.如果5个人被录用的机会相等,分别计算下列事件的概率;
(1)女孩A得到一个职位;
(2)女孩A和B各得到一个职位;
(3)女孩A或B得到一个职位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆C:
的椭圆C:![]() (a>b>0)的左焦点为
(a>b>0)的左焦点为![]() ,过
,过![]() 作长轴的垂线交椭圆于
作长轴的垂线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.
(I)求椭圆C的标准方程;
(II)设O为原点,若点A在直线![]() 上,点B在椭圆C上,且
上,点B在椭圆C上,且![]() ,求线段AB长度的最小值.
,求线段AB长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com