
【题目】设抛物线的顶点在坐标原点,焦点F在![]() 轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到
轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到![]() 轴的距离是
轴的距离是![]() .
.
(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点P,使得过点P的直线交抛物线于另一点Q,满足![]() ,且直线PQ与抛物线在点P处的切线垂直?并请说明理由.
,且直线PQ与抛物线在点P处的切线垂直?并请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知下列三个命题:
①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的 ![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆 ![]() 相切.
相切.
其中真命题的序号是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
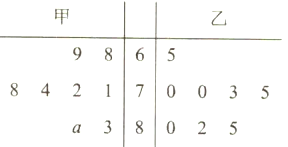
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x 的焦点为F.
(1)点A,P满足 ![]() .当点A在抛物线C上运动时,求动点P的轨迹方程;
.当点A在抛物线C上运动时,求动点P的轨迹方程;
(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com