
����Ŀ����������{an}�����ӵڶ������ÿһ������ڸ���֮ǰ��������ĺͣ����{an}ΪP����.
��1����{an}��ǰn���Sn��3n+2�����ж�{an}�Ƿ���P���У���˵�����ɣ�
��2��������a1��a2��a3������a10������Ϊ��1������Ϊd�ĵȲ����У�����������P���У���d��ȡֵ��Χ��
��3������������{an}������Ϊa������Ϊq�ĵȱ����У���������{bn}��{cn}�Ǵ�{an}��ȡ�������ԭ����˳������ɵIJ�ͬ���У���������ͷֱ�ΪT1��T2����{an}��P����ʱa��q���������������֤����������a��0��T1��T2����{an}����P������.
���𰸡���1������{an}��P���У����������2��![]() ��3��
��3��![]() ��
�� ��֤��������
��֤��������
��������
��1����������е�ͨ�ʽ��Ȼ����P���е��ص������֤��
��2����������е�ͨ�ʽ��Ȼ����P���е��ص��г����ȹ�ϵ��Ȼ�������⣻
��3������P���н������ȹ�ϵ����ⲻ��ʽ�ɵ�.
��1����![]() ��
��
��![]() ��
��
��n��1ʱ��a1��S1��5��
��![]() ��
��
��ô��![]() ʱ��
ʱ��![]() ���������⣬
���������⣬
������{an}��P����.
��2��������֪�������е�ǰn���Ϊ![]() ��
��
������a1��a2��a3������a10��P���У���֪a2��S1��a1���ʹ���d��0��
![]() ������n��1��2��3��
������n��1��2��3��![]() ��9������n����������
��9������n����������![]() �����
�����![]() ��
��
��d��ȡֵ��ΧΪ![]() .
.
��3������{an}��P������a��S1��a2��aq��
��a��0����q��1������an+1��Sn��һ��������n����������֪![]() ����
����![]() ��һ��������n��������
��һ��������n��������
��![]() ����2��q��0���ɵ�q��2����
����2��q��0���ɵ�q��2����
��a��0����q��1������an+1��Sn��һ��������n����������֪![]() ������2��q��qn��1��һ��������n��������
������2��q��qn��1��һ��������n��������
�ֵ�q�ʣ���������1]ʱ����2��q��qn��1��n��2ʱ��������
����![]() ��
��![]() �����
�����![]() ��
��
�൱{an}��P����ʱ��a��q���������Ϊ![]() ��
�� ��
��
�ڼ���{an}��P���У����ɢٿ�֪��q��2��a��0����{an}��ÿһ���Ϊ������
��{bn}�е�ÿһ���{cn}�У��������������Dz�ͬ���У���֪T1��T2��
��{cn}�е�ÿһ���{bn}�У�ͬ���ɵ�T1��T2��
��{bn}��������һ���{cn}����{cn}��������һ���{bn}�У�
��{bn'}��{cn'�ǽ�{bn}��{cn}�еĹ�����ȥ��֮��ʣ�������ι��ɵ����У����ǵ�������ͷֱ�ΪT1'��T2'��
������{bn'}��{cn'}����������{bn'}�У���Ϊam��m��2����
��T2'��a1+a2+����+am��1��am��T1'����T2'��T1'��������T1��T2��T1��T2ì�ܣ��ʼ������ԭ������ȷ.


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1��������![]() ��������ֵ�㣬��ʵ��
��������ֵ�㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ������
������![]() ʱ������
ʱ������![]() ��������ֵ��
��������ֵ��![]() ����
����![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹᳹��ʵ����ʡ�й�������״��������������ع���Ҫ����Ӧ������״�������飬��ʵ����2020�괺����ѧ����������У��ȫ�ȶ����ռ�����֪ʶ��ȷ��ʦ��������ȫ�����彡��.ijУ��ѧǰ����֯�����꼶800��ѧ���μ��ˡ�������ء�����֪ʶ����(����150��).��֪��800��ѧ���ijɼ���������90�֣�����800��ѧ���ijɼ��������£���һ��![]() ���ڶ���
���ڶ���![]() ��������
��������![]() ��������
��������![]() ��������
��������![]() ��������
��������![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
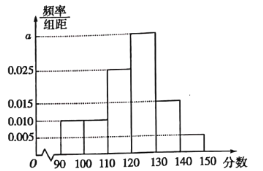
��1����![]() ��ֵ��������800��ѧ����ƽ���ɼ�(ͬһ���е������ø���������е�ֵ����)��
��ֵ��������800��ѧ����ƽ���ɼ�(ͬһ���е������ø���������е�ֵ����)��
��2����У��Ⱥ��Ⱥ�ء�������Ϊ���õض��ٸ���ѧ���ġ����˷��ء���������800��ѧ����ȡ2��ѧ�����붽�鹤������ȡ�취�ǣ����ڵڶ����������������÷ֲ�����ķ�����ȡ6��ѧ�����ٴ���6��ѧ���������ȡ2��ѧ��.����2��ѧ���ľ����ɼ��ֱ�Ϊ![]()
![]() .���¼�
.���¼�![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() �ϵĶ���
�ϵĶ���![]() ����
����![]() �ľ�����������
�ľ�����������![]() �ľ����3��.
�ľ����3��.
��1�����![]() �����ꣻ
�����ꣻ
��2����˫����![]() ���ҽ�����
���ҽ�����![]() ��˫���߾�������
��˫���߾�������![]() ����
����![]() ����˫���ߵķ��̣�
����˫���ߵķ��̣�
��3����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() �������ܷ��ҵ�һ��б��Ϊ
�������ܷ��ҵ�һ��б��Ϊ![]() ��
��![]() ����ֱ��
����ֱ��![]() �루2���е�˫����
�루2���е�˫����![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() ��������
��������![]() �������ڣ����б��
�������ڣ����б��![]() ��ȡֵ��Χ���������ڣ���˵������.
��ȡֵ��Χ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�һ��������װ�����ſ�Ƭ���ֱ���������![]() ��
��![]() ��
��![]() �������ſ�Ƭ����ǵ���������ȫ��ͬ������зŻصس�ȡ
�������ſ�Ƭ����ǵ���������ȫ��ͬ������зŻصس�ȡ![]() �Σ�ÿ�γ�ȡ
�Σ�ÿ�γ�ȡ![]() �ţ�����ȡ�Ŀ�Ƭ�ϵ��������μ�Ϊ
�ţ�����ȡ�Ŀ�Ƭ�ϵ��������μ�Ϊ![]() ��
��![]() ��
��![]() .
.
������������ȡ�Ŀ�Ƭ�ϵ���������![]() ���ĸ��ʣ�
���ĸ��ʣ�
������������ȡ�Ŀ�Ƭ�ϵ�����![]() ��
��![]() ��
��![]() ����ȫ��ͬ���ĸ���.
����ȫ��ͬ���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��1��������![]() �ǵȱ����У����ж�����
�ǵȱ����У����ж�����![]() �Ƿ�Ϊ�ȱ����У���˵�����ɣ�
�Ƿ�Ϊ�ȱ����У���˵�����ɣ�
��2����![]() ǡ����һ���Ȳ����е�ǰ
ǡ����һ���Ȳ����е�ǰ![]() ��ͣ���֤������
��ͣ���֤������![]() �ǵȲ����У�
�ǵȲ����У�
��3��������![]() �Ǹ����Ϊ�����ĵȱ����У�����
�Ǹ����Ϊ�����ĵȱ����У�����![]() �ǵȲ����У���֤������
�ǵȲ����У���֤������![]() �ǵȲ����У�
�ǵȲ����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ����Բ
����Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() .
.
��1�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() �Ĵ�ֱƽ������
�Ĵ�ֱƽ������![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֤��
����֤��![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com