
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 
A.4
B.5
C.6
D.7
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=aln(x2+1)+bx存在两个极值点x1 , x2 .
(1)求证:|x1+x2|>2;
(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,试求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴,
轴,![]() 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为![]() 该椭圆的离心率为
该椭圆的离心率为![]()
(1)求椭圆的方程
(2)是否存在过点P(![]() 的直线
的直线![]() 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
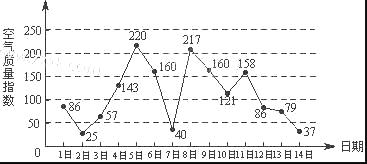
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+bx﹣c,f(x)在点(1,f(1))处的切线方程为x+y+4=0.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)若在区间 ![]() 内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A1 , B1分别是边BA,CB的中点,A2 , B2分别是线段A1A,B1B的中点,…,An , Bn分别是线段 ![]() 的中点,设数列{an},{bn}满足:向量
的中点,设数列{an},{bn}满足:向量 ![]() ,有下列四个命题,其中假命题是( )
,有下列四个命题,其中假命题是( )
A.数列{an}是单调递增数列,数列{bn}是单调递减数列
B.数列{an+bn}是等比数列
C.数列 ![]() 有最小值,无最大值
有最小值,无最大值
D.若△ABC中,C=90°,CA=CB,则 ![]() 最小时,
最小时, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}.满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后成等比数列,an+2log2bn=﹣1.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点![]() ,且与圆
,且与圆![]() 外切于点
外切于点![]() ,
,![]() 是x轴上的一个动点.
是x轴上的一个动点.
![]() 求圆C的标准方程;
求圆C的标准方程;
![]() 当圆C上存在点Q,使
当圆C上存在点Q,使![]() ,求实数m的取值范围;
,求实数m的取值范围;
![]() 当
当![]() 时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且
时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且![]() 求证:直线AB恒过定点.
求证:直线AB恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com