
【题目】已知△ABC,|AB|=8,AC与BC边所在直线的斜率之积为定值m,
(1)求动点C的轨迹方程;
(2)当m=1时,过点E(0,1)的直线l与曲线C相交于P、Q两点,求P、Q两点的中点M的轨迹方程.
【答案】
(1)解:以AB边所在直线为x轴,以AB边的垂直平分线为y轴建立平面直角坐标系
则A(﹣4,0),B(4,0)
设点C的坐标为(x,y),则 ![]() ,
,
∴ ![]() ,
,
即mx2﹣y2=16m
当m=0时,动点C的轨迹方程为y=0(x≠±4),
表示x轴所在直线去掉A、B两点剩下的部分
当m>0时,动点C的轨迹方程为 ![]()
表示焦点在x轴上的双曲线去掉A、B两点剩下的部
当﹣1<m<0时,动点C的轨迹方程为 ![]()
表示焦点在x轴上的椭圆去掉A、B两点剩下的部分
当m<﹣1时,动点C的轨迹方程为 ![]()
表示焦点在y轴上的椭圆去掉A、B两点剩下的部分
当m=﹣1时,动点C的轨迹方程为 x2+y2=16(x≠±4)
表示以AB为直径的圆去掉A、B两点剩下的部分
(2)解:当m=1时,动点C的轨迹方程为 ![]() ,
,
当直线l的斜率不存在时,显然不可能与 ![]() 有交点,舍去;
有交点,舍去;
当直线l的斜率存在时,设l的方程为y=kx+1,设P(x1,y1),Q(x2,y2),M(x0,y0)
联立方程组  ,
,
消去y得:(1﹣k2)x2﹣2kx﹣17=0
由题意得:x1、x2是此方程的解
所以 ![]() ∴
∴ ![]()
所以 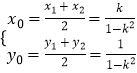
![]() ,所以得
,所以得 ![]() 又直线l与动点C的轨迹方程有两个不同的焦点,
又直线l与动点C的轨迹方程有两个不同的焦点,
则  ∴
∴ ![]() 且
且 ![]() 且k2≠1,∴
且k2≠1,∴ ![]() 或y0<﹣16
或y0<﹣16
所以P、Q两点的中点M的轨迹方程为 ![]()
【解析】(1)以AB边所在直线为x轴,以AB边的垂直平分线为y轴建立平面直角坐标系,利用AC与BC边所在直线的斜率之积为定值m,建立方程,即可求动点C的轨迹方程;(2)分类讨论,联立方程组,即可求P、Q两点的中点M的轨迹方程.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的方程为:x2+y2=4
(1)求过点P(2,1)且与圆C相切的直线l的方程;
(2)直线l过点D(1,2),且与圆C交于A、B两点,若|AB|=2 ![]() ,求直线l的方程;
,求直线l的方程;
(3)圆C上有一动点M(x0 , y0), ![]() =(0,y0),若向量
=(0,y0),若向量 ![]() =
= ![]() +
+ ![]() ,求动点Q的轨迹方程.
,求动点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为2,4,4.现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
( II)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=4与x轴负半轴的交点为A,点P在直线l: ![]() x+y﹣a=0上,过点P作圆O的切线,切点为T
x+y﹣a=0上,过点P作圆O的切线,切点为T
(1)若a=8,切点T( ![]() ,﹣1),求点P的坐标;
,﹣1),求点P的坐标;
(2)若PA=2PT,求实数a的取值范围;
(3)若不过原点O的直线与圆O交于B,C两点,且满足直线OB,BC,OC的斜率依次成等比数列,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)写出函数f(x)(x∈R)的解析式.
(2)若函数g(x)=f(x)+(4﹣2a)x+2(x∈[1,2]),求函数g(x)的最小值h(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点,例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点,若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是( )
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点,例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点,若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是( )
A.[﹣1,1]
B.(0,2)
C.[﹣2,2]
D.(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com