
【题目】已知椭圆 ![]() 与y轴交于B1、B2两点,F1为椭圆C的左焦点,且△F1B1B2是腰长为
与y轴交于B1、B2两点,F1为椭圆C的左焦点,且△F1B1B2是腰长为 ![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆C的方程;
(2)设直线x=my+1与椭圆C交于P、Q两点,点P关于x轴的对称点为P1(P1与Q不重合),则直线P1Q与x轴是否交于一个定点?若是,请写出该定点坐标,并证明你的结论;若不是,请说明理由.
【答案】
(1)解:椭圆 ![]() 与y轴交于B1、B2两点,
与y轴交于B1、B2两点,
F1为椭圆C的左焦点,且△F1B1B2是腰长为 ![]() 的等腰直角三角形.可得b=c,a=
的等腰直角三角形.可得b=c,a= ![]() ,则b=1,
,则b=1,
椭圆C的方程: ![]()
(2)解:设P(x1,y1)Q(x2,y2)P1(x1,﹣y1)
由直线x=my+1与 ![]() 联立得,(m2+2)y2+2my﹣1=0
联立得,(m2+2)y2+2my﹣1=0
韦达定理得, ![]()
而直线PQ的方程为 ![]() ,令y=0,则
,令y=0,则 ![]() ,
,
所以直线PQ过定点(2,0)
【解析】(1)利用已知条件求出b=c,a= ![]() ,则b=1,推出椭圆C的方程.(2)设P(x1 , y1),Q(x2 , y2),P1(x1 , ﹣y1)联立x=my+1与
,则b=1,推出椭圆C的方程.(2)设P(x1 , y1),Q(x2 , y2),P1(x1 , ﹣y1)联立x=my+1与 ![]() ,利用韦达定理得,转化求解直线方程,即可推出结果.
,利用韦达定理得,转化求解直线方程,即可推出结果.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy内,动点P到定点F(﹣1,0)的距离与P到定直线x=﹣4的距离之比为 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设点A、B是轨迹C上两个动点,直线OA、OB与轨迹C的另一交点分别为A1、B1 , 且直线OA、OB的斜率之积等于- ![]() ,问四边形ABA1B1的面积S是否为定值?请说明理由.
,问四边形ABA1B1的面积S是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y= ![]() (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( ) 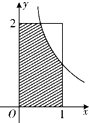
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)已知命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
A.﹣2≤a≤1
B.a≤﹣2或1≤a≤2
C.a≥1
D.a≤﹣2或 a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 1.3 | 1.9 | 2.5 | 2.7 | 3.6 |
(1)画出散点图;
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com