
【题目】已知锐角△ABC中,内角![]() 所对应的边分别为
所对应的边分别为![]() ,且满足:
,且满足:![]() ,
,![]() ,则
,则![]() 的取值范围是____________.
的取值范围是____________.
【答案】![]()
【解析】分析:由已知可得:b2=2a+a2,又由余弦定理可得:b2=a2+4-4acosB,整理可得:![]() ,可求B的范围,进而可求cosB的范围,进而可求a的范围.
,可求B的范围,进而可求cosB的范围,进而可求a的范围.
详解::∵b2-a2=ac,c=2,可得:b2=2a+a2,又∵由余弦定理可得:b2=a2+c2-2accosB=a2+4-4acosB,
∴2a+a2=a2+4-4acosB,整理可得:![]() ,∵由余弦定理2bccosA=b2+c2-a2=c2+ac,可得:2bcosA=c+a,
,∵由余弦定理2bccosA=b2+c2-a2=c2+ac,可得:2bcosA=c+a,
∴由正弦定理可得:2sinBcosA=sinC+sinA=sin(A+B)+sinA=sinAcosB+cosAsinB+sinA,
可得:sinBcosA-sinAcosB=sinA,可得:sin(B-A)=sinA,可得:B-A=A,或B-A=π-A(舍去),可得:B=2A,C=π-A-B=π-3A,由△ABC为锐角三角形,可得: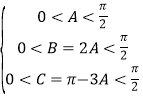 解得:
解得:![]() 可得:cosB∈
可得:cosB∈![]() ,∴可得:1+2cosB∈(1,2),
,∴可得:1+2cosB∈(1,2),![]() ∈(1,2),故答案为:(1,2).
∈(1,2),故答案为:(1,2).


科目:高中数学 来源: 题型:
【题目】过 ![]() 轴上动点
轴上动点 ![]() 引抛物线
引抛物线 ![]() 的两条切线
的两条切线 ![]() 、
、 ![]() ,
, ![]() 、
、 ![]() 为切点,设切线
为切点,设切线 ![]() 、
、 ![]() 的斜率分别为
的斜率分别为 ![]() 和
和 ![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:直线 ![]() 恒过定点,并求出此定点坐标;
恒过定点,并求出此定点坐标;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体![]() 中,O是坐标原点,OA是
中,O是坐标原点,OA是![]() 轴,OC是
轴,OC是![]() 轴,
轴,![]() 是
是![]() 轴.E是AB中点,F是
轴.E是AB中点,F是![]() 中点,OA=3,OC=4,
中点,OA=3,OC=4,![]() =3,则F坐标为( )
=3,则F坐标为( )
A. (3,2,![]() ) B. (3,3,
) B. (3,3,![]() )
)
C. (3,![]() ,2) D. (3,0,3)
,2) D. (3,0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的角A,B,C所对的边分别为a,b,c,设向量![]() =(a,b),
=(a,b),![]() =(sin B,sin A),
=(sin B,sin A), ![]() =(b-2,a-2).
=(b-2,a-2).
(1)若![]() ∥
∥![]() ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若![]() ⊥
⊥![]() ,边长c=2,∠C=
,边长c=2,∠C=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com