
【题目】已知集合![]() .
.
(1)若![]() 是
是![]() 的充分条件,求
的充分条件,求![]() 的取值范围.
的取值范围.
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
求解二次不等式化简集合![]() .(1)对
.(1)对![]() 分类求解集合
分类求解集合![]() ,然后把
,然后把![]() 是
是![]() 的充分条件转化为含有
的充分条件转化为含有![]() 的不等式组,即可求解
的不等式组,即可求解![]() 的范围;(2)由
的范围;(2)由![]() ,借助于集合
,借助于集合![]() ,
,![]() 的端点值间的关系列不等式求解
的端点值间的关系列不等式求解![]() 的范围.
的范围.
A={x|x2-6x+8<0}={x|2<x<4},
B={x|(x-a)(x-3a)<0}.
(1)当a=0时,B=,不合题意.
当a>0时,B={x|a<x<3a},要满足题意,
则![]() ,解得
,解得![]() ≤a≤2.
≤a≤2.
当a<0时,B={x|3a<x<a},要满足题意,
则![]() ,无解.
,无解.
综上,a的取值范围为![]() .
.
(2)要满足A∩B=,
当a>0时,B={x|a<x<3a}
则a≥4或3a≤2,即0<a≤![]() 或a≥4.
或a≥4.
当a<0时,B={x|3a<x<a},
则a≤2或a≥![]() ,即a<0.
,即a<0.
当a=0时,B=,A∩B=.
综上,a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: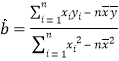 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且
,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且![]() .
.
(1)求抛物线的标准方程;
(2)对于抛物线上任一点Q,点P(2t,0)都满足|PQ|≥2|t|,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1,y1),D(x2,y2)其中(x1<x2)是曲线y2=9x(y≥0).上的两点,A,D两点在x轴上的射影分别为点B,C且|BC|=3.
(Ⅰ)当点B的坐标为(1,0)时,求直线AD的方程:
(Ⅱ)记△AOD的面积为S1,梯形ABCD的面积为S2,求![]() 的范围
的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() 是正数
是正数
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为定值;
的夹角为定值;
(3)当![]() 时,把
时,把![]() 中所有与
中所有与![]() 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为![]() ,令
,令![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的极限点
的极限点![]() 的坐标.(注:若点坐标为
的坐标.(注:若点坐标为![]() ,且
,且![]() ,则称点
,则称点![]() 为点列的极限点)
为点列的极限点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,其中
,其中![]() 是自然常数,
是自然常数, ![]() .
.
(1)当![]() 时,求
时,求![]() 的极值,并证明
的极值,并证明![]() 恒成立;
恒成立;
(2)是否存在实数![]() ,使
,使![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() ,
,![]() (0,
(0,![]() )为
)为![]() 型函数,共中
型函数,共中![]() .
.
(1)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 的值域;
的值域;
(2)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 极值点个数;
极值点个数;
(3)若![]() 是
是![]() 型函数,在
型函数,在![]() 上有三点A、B、C横坐标分別为
上有三点A、B、C横坐标分別为![]() 、
、![]() 、
、![]() ,其中
,其中![]() <
<![]() <
<![]() ,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
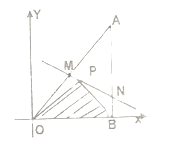
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com