
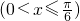 ,四边形BCEF面积为y,则函数y=f(x)的图象大致是
,四边形BCEF面积为y,则函数y=f(x)的图象大致是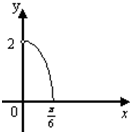
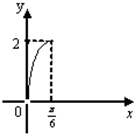
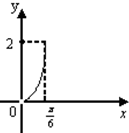
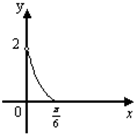
 表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.
表示出GH,再利用四边形BCEF面积为y=BC×GH求出f(x),根据解析式作简图,与选项对应.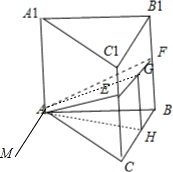 过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=
过A作AM∥BC,H,G是BC,EF中点,则 AH⊥BC,∴AH⊥AM,在等腰三角形△AEF中,AG⊥EF,∵EF∥BC.∴AG⊥AM,∴∠GAH是平面α与底面ABC所成二面角的平面角.∴∠GAH=x,tanx=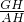 ,∴GH=
,∴GH= tanx
tanx tanx,根据正切函数图象可知C符合.
tanx,根据正切函数图象可知C符合.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
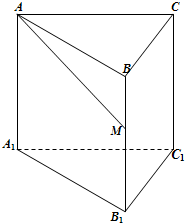 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| AM |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
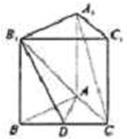 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com