
【题目】已知函数![]() .
.
(1)求证:当![]() 时,函数
时,函数![]() 在
在![]() 上,存在唯一的零点;
上,存在唯一的零点;
(2)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)(0,1).
【解析】试题分析:(1)先证明函数![]() 在(0,+∞)上单调递增,再根据零点存在定理证明
在(0,+∞)上单调递增,再根据零点存在定理证明![]() 上存在零点即可。(2)“若存在
上存在零点即可。(2)“若存在![]() ,使得
,使得![]() 成立”转化为
成立”转化为
“![]() ”,利用导数可得
”,利用导数可得![]()
![]() ,从而由
,从而由![]() 得
得![]() ,设g(a)=lna+a﹣1,由g(a)的单调性可得当0<a<1时,g(a)<0,故所求范围为(0,1)。
,设g(a)=lna+a﹣1,由g(a)的单调性可得当0<a<1时,g(a)<0,故所求范围为(0,1)。
试题解析:
(1)证明:∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴函数f(x)在(0,+∞)上单调递增,
又当a≤0时, ![]() ,
, ![]() ,
,
所以函数![]() 上存在唯一零点。
上存在唯一零点。
(2)由(1)得![]() ,
,
∵a>0,
∴当x∈(0, ![]() )时,f′(x)>0,f(x)单调递增;
)时,f′(x)>0,f(x)单调递增;
当x∈(![]() ,+∞)时,f′(x)<0,f(x)单调递减。
,+∞)时,f′(x)<0,f(x)单调递减。
∴![]() 在x=
在x=![]() 时取得最大值,且最大值为
时取得最大值,且最大值为![]() 。
。
“存在![]() ”等价于
”等价于![]()
![]()
∴![]() ,
,
∴![]() ,
,
令g(a)=lna+a﹣1
∵g(a)在(0,+∞)单调递增,且g(1)=0,
∴当0<a<1时,g(a)<0;当a>1时,g(a)>0。
∴a的取值范围为(0,1)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示: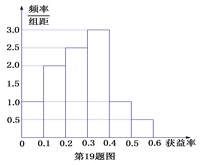
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在 ![]() 元的基础上每增加
元的基础上每增加 ![]() 元,对应的销量
元,对应的销量 ![]() (万份)与
(万份)与 ![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下 ![]() 组
组 ![]() 与
与 ![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量 ![]() (万份)与
(万份)与 ![]() (元)的回归方程为
(元)的回归方程为 ![]() ;
;
(ⅱ)若把回归方程 ![]() 当作
当作 ![]() 与
与 ![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,若函数
,若函数 ![]() 满足下列两个条件,则称
满足下列两个条件,则称 ![]() 在定义域
在定义域 ![]() 上是闭函数.①
上是闭函数.① ![]() 在
在 ![]() 上是单调函数;②存在区间
上是单调函数;②存在区间 ![]() ,使
,使 ![]() 在
在 ![]() 上值域为
上值域为 ![]() .如果函数
.如果函数 ![]() 为闭函数,则
为闭函数,则 ![]() 的取值范围是.
的取值范围是.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量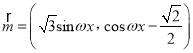 ,
, 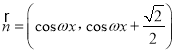 (
(![]() ),若
),若![]() ,且
,且![]() 的图象上两相邻对称轴间的距离为
的图象上两相邻对称轴间的距离为![]() .
.
(Ⅰ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)设![]() 的内角
的内角![]() ,
, ![]() ,
, ![]() 的对边分别为
的对边分别为![]() ,
, ![]() ,
, ![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() ,求
,求![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4,坐标系与参数方程]
在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]()
![]() ,以坐标原点为极点,以
,以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的直角坐标方程和曲线C的普通方程。
的直角坐标方程和曲线C的普通方程。
(2)设点P为曲线C上的任意一点,求点P到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 的方程为
的方程为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
【答案】(I)证明见解析;(II)![]() ;(III)2018.
;(III)2018.
【解析】试题分析:
(1)左右两侧做差,结合代数式的性质可证得![]() ,即对
,即对![]() ,恒有:
,恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,给定特殊值,令
,给定特殊值,令![]() ,从而可得:
,从而可得:![]() ,则
,则![]() ,
,![]() ,从而有
,从而有![]() 恒成立,据此可知
恒成立,据此可知![]() ,则
,则![]() .
.
(3)结合(1)(2)的结论整理计算可得:![]() ,据此分组求和有:
,据此分组求和有:![]() .
.
试题解析:
(1)![]() (仅当
(仅当![]() 时,取“=”)
时,取“=”)
所以恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,则
,则![]() 中,令
中,令![]() ,
,
从而可得:![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因为![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,不合题意舍去,
,不合题意舍去,
当![]() 时,即
时,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(3)![]() ,
,
所以![]() ,
,
即![]() .
.
【题型】解答题
【结束】
22
【题目】已知函数![]() 为定义在
为定义在![]() 上的奇函数.
上的奇函数.
(1)求函数![]() 的值域;
的值域;
(2)当![]() 时,不等式
时,不等式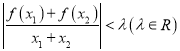 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com