分析:(1)欲证AB1∥平面DBC1,根据直线与平面平行的判定定理可知只需证AB1与平面DBC1内一直线平行,根据等腰三角形可知DE∥AB1,又AB1∉平面DBC1,DE?平面DBC1,满足定理所需条件;
(2)作DF⊥BC,垂足为F,则DF⊥面B1BCC1,连接EF,则EF是ED在平面B1BCC1上的射影,根据二面角的平面角的定义可知∠DEF是二面角α的平面角,然后在三角形DEF中求出∠DEF即可.
解答: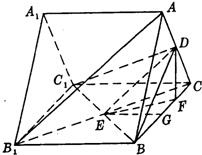
(1)证明:
∵A
1B
1C
1-ABC是正三棱柱,∴四边形B
1BCC
1是矩形.
连接B
1C交BC
1于E,则B
1E=EC.连接DE.
在△AB
1C中,∵AD=DC,∴DE∥AB
1.
又AB
1?平面DBC
1,DE?平面DBC
1,∴AB
1∥平面DBC
1.
(2)解:作DF⊥BC,垂足为F,
则DF⊥面B
1BCC
1,连接EF,
则EF是ED在平面B
1BCC
1上的射影.
∵AB
1⊥BC
1,
由(1)知AB
1∥DE,∴DE⊥BC
1,则BC
1⊥EF,∴∠DEF是二面角α的平面角.
设AC=1,则DC=
.∵△ABC是正三角形,∴在Rt△DCF中,
DF=DC•sinC=
,CF=DC•cosC=
.取BC中点G.∵EB=EC,∴EG⊥BC.
在Rt△BEF中,
EF
2=BF•GF,又BF=BC-FC=
,GF=
,
∴EF
2=
•
,即EF=
.∴tan∠DEF=
==1.∴∠DEF=45°.
故二面角α为45°.
点评:本小题考查空间线面关系、正棱柱的性质、空间想象能力和逻辑推理能力,属于中档题.

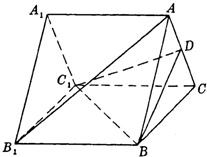
 (1)证明:
(1)证明:

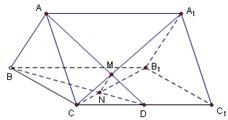 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN. (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F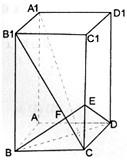 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.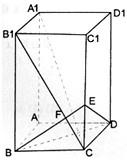 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C. 如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F