
【题目】如图,在四棱锥P﹣ABCD中,PA=PB,PA⊥PB,AB⊥BC,且平面PAB⊥平面ABCD,若AB=2,BC=1, ![]() .
.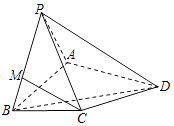
(1)求证:PA⊥平面PBC;
(2)若点M在棱PB上,且PM:MB=3,求证CM∥平面PAD.
【答案】
(1)证明:∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,BC⊥AB,
∴BC⊥平面PAB,又PA平面PAB,
∴BC⊥PA,
又PA⊥PB,PB∩BC=B,PB平面PBC,BC平面PBC,
∴PA⊥平面PBC.
(2)在AB上取点N,使得AN:BN=3,取AB的中点O,连结MN,CN,PO,OD,
∵ ![]() ,
,

∴MN∥PA.
由(1)知BC⊥平面PAB,∴BC⊥BN,
∵BN= ![]() AB=
AB= ![]() ,BC=1,∴tan∠BNC=
,BC=1,∴tan∠BNC= ![]() .
.
∵AD=BD= ![]() ,AB=2,O是AB的中点,
,AB=2,O是AB的中点,
∴OD⊥AB,OA=1,OD= ![]() =2,
=2,
∴tan∠OAD= ![]() ,
,
∴∠BNC=∠OAD,∴CN∥AD,
又MN∩CN,PA∩AD=A,
∴平面MNC∥平面PAD.
又∵CM平面MNC,
∴CM∥平面PAD.
【解析】(1)先利用面面垂直的性质定理可证BC⊥平面PAB,进而可证BC⊥PA,再利用线面垂直的判定定理可证PA⊥平面PBC;(2)先在AB上取点N,使得AN:BN=3,取AB的中点O,连结MN,CN,PO,OD,进而可证MN∥PA,再证CN∥AD,进而可证平面MNC∥平面PAD,从而可证CM∥平面PAD.
【考点精析】关于本题考查的直线与平面平行的判定和平面与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】按如图所示的程序框图操作: (Ⅰ)写出输出的数所组成的数集.若将输出的数按照输出的顺序从前往后依次排列,则得到数列{an},请写出数列{an}的通项公式;
(Ⅱ)如何变更A框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{2n}的前7项?
(Ⅲ)如何变更B框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣2alnx+(a﹣2)x,a∈R.
﹣2alnx+(a﹣2)x,a∈R.
(1)当a=﹣1时,求函数f(x)的极值;
(2)当a<0时,讨论函数f(x)单调性;
(3)是否存在实数a,对任意的m,n∈(0,+∞),且m≠n,有 ![]() >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.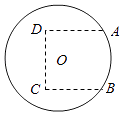
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为 . 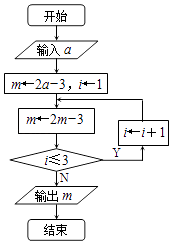
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BCAE=DCAF,B,E,F,C四点共圆.证明:CA是△ABC外接圆的直径.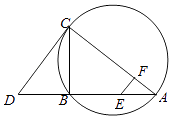
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,已知平面PBC⊥平面ABC.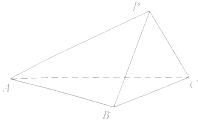
(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA:
(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年5月17日为国际电信日,某市电信公司每年在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.根据以往的统计结果绘出电信日当天参与活动的统计图,现将频率视为概率.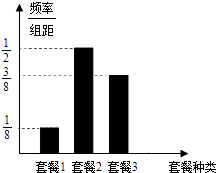
(1)求某两人选择同一套餐的概率;
(2)若用随机变量X表示某两人所获优惠金额的总和,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com