
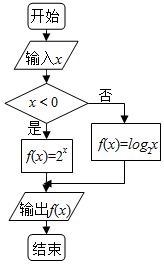
 如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].
如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$]. 分析 由程序框图得出函数y=f(x)的解析式,并根据其单调性求出相应的自变量x的取值范围即可.
解答 解:由程序框图可知:f(x)=$\left\{\begin{array}{l}{{2}^{x}}&{x≤0}\\{lo{g}_{2}x}&{x>0}\end{array}\right.$,
∵输出的函数值在区间[-2,$\frac{1}{2}$]内,
∴必有当x≤0时,0<2x≤$\frac{1}{2}$;
当x>0时,-2≤log2x≤$\frac{1}{2}$.
解得x≤-1或$\frac{1}{4}$≤x≤$\sqrt{2}$.
故答案为:(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].
点评 本题主要考查了程序框图的应用,正确理解程序框图的功能是解题的关键,属于基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某商场连续10天对甲商品每天的销售量(单位:件)进行了统计,得到如图所示的茎叶图,据该图估计商店一天的销售量不低于40件的频率为( )
某商场连续10天对甲商品每天的销售量(单位:件)进行了统计,得到如图所示的茎叶图,据该图估计商店一天的销售量不低于40件的频率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com