
分析 由数列{an}的通项${a_n}=2n•({{{cos}^2}\frac{nπ}{3}-{{sin}^2}\frac{nπ}{3}})$可求得,a1+a2+a3=a4+a5+a6=…=a28+a29+a30=3,从而可得答案.
解答 解:∵${a_n}=2n•({{{cos}^2}\frac{nπ}{3}-{{sin}^2}\frac{nπ}{3}})$,
∴a1=2(${cos}^{2}\frac{π}{3}$-${sin}^{2}\frac{π}{3}$)=-1;
a2=4(${cos}^{2}\frac{2π}{3}$-${sin}^{2}\frac{2π}{3}$)=-2;
a3=6(cos2π-sin2π)=6;
∴a1+a2+a3=3;
同理可得,a4+a5+a6=3;
…,
a28+a29+a30=3;
∴S30=10×3=30.
故答案为:30.
点评 本题考查数列的求和,求得a1+a2+a3=a4+a5+a6=…=a28+a29+a30=3是关键,考查运算与推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
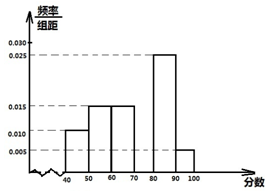 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
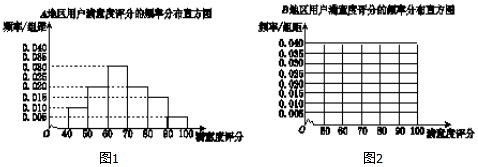
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 14 | 10 | 6 |
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A与B | B. | B与C | C. | A与D | D. | C与D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com