
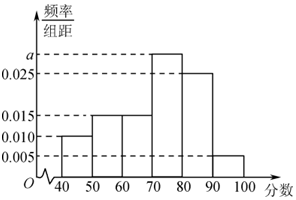
 ijУ�Ӹ�һ�꼶ѧ���������ȡ100��ѧ�������������п��Ե���ѧ�ɼ�����Ϊ�������ֳ����Σ�[40��50����[50��60������[90��100������õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
ijУ�Ӹ�һ�꼶ѧ���������ȡ100��ѧ�������������п��Ե���ѧ�ɼ�����Ϊ�������ֳ����Σ�[40��50����[50��60������[90��100������õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������ ��1����Ƶ�ʷֲ�ֱ��ͼ�����������[70��80���ڵĸ��ʣ��ɴ������������[70��80���е�������
��2��������[40��50����ѧ����10�ˣ�������[50��60����ѧ����15�ˣ��ɴ�������÷ֲ�����ķ����ӷ�����[40��50����[50��60����ѧ���й���ȡ5 �ˣ���ȡ��5���з�����[40��50����������
��3���÷ֲ�����ķ����ӷ�����[40��50����[50��60����ѧ���й���ȡ5 �ˣ���ȡ��5���з�����[40��50������2�˷�����[50��60������3�ˣ��ɴ����õȿ����¼����ʼ��㹫ʽ�����������[40��50����[50��60����1 �˵ĸ��ʣ�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ֪С���������Ϊ��Ӧ������ʣ�
����С�����������Ϊ1����˷�����[70��80���ڵĸ���Ϊ��
1-��0.005+0.010+0.015��2+0.025����10=0.3��
�������[70��80���е�����Ϊ��0.3��100=30�ˣ���5��
��2��������[40��50����ѧ���У�0.010��10��100=10�ˣ�
������[50��60����ѧ���У�0.015��10��100=15�ˣ�
�÷ֲ�����ķ����ӷ�����[40��50����[50��60����ѧ���й���ȡ5 �ˣ�
��ȡ��5���з�����[40��50�������У�5��$\frac{10}{10+15}$=2�ˣ���9��
��3��������[40��50����ѧ����10�ˣ�������[50��60����ѧ����15�ˣ�
�÷ֲ�����ķ����ӷ�����[40��50����[50��60����ѧ���й���ȡ5 �ˣ�
��ȡ��5���з�����[40��50������2�˷�����[50��60������3�ˣ�
5���������ȡ2 �˹���n=${C}_{5}^{2}$=10�ֿ��ܣ�
�ֱ��ڲ�ͬ��������m=${C}_{2}^{1}{C}_{3}^{1}$=6�ֿ��ܣ�
���Է�����[40��50����[50��60����1 �˵ĸ���P=$\frac{6}{10}$=$\frac{3}{5}$��14�֣�
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ���ֲ������Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע��ȿ����¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ͦ£���ô����һ������ֱ��ƽ���ڦ� | |
| B�� | ������ͦã��¡ͦã����ɦ�=l����ôl�ͦ� | |
| C�� | ���������ֱ�ڦ£���ô����һ��������ֱ�ߴ�ֱ�ڦ� | |
| D�� | ������ͦ£���ô��������ֱ�߶���ֱ�ڦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{x^2}$ | B�� | $-\frac{1}{x^2}$ | C�� | $\frac{1}{2x}$ | D�� | $-\frac{1}{2x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
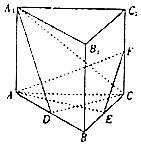 ��ͼ������������ABC-A1B1C1�У�E��F�ֱ���BC��CC1���е㣮
��ͼ������������ABC-A1B1C1�У�E��F�ֱ���BC��CC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com