
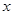 表示.
表示.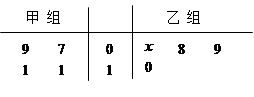
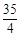 ,求
,求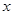 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;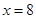 ,方差
,方差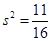 .(2)
.(2)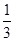 .
.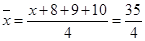 ,得
,得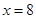 ,
,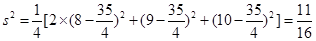 .
.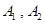 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.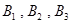 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.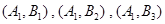 ,
, 共6种. 9分
共6种. 9分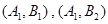 共2种.
共2种.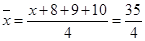 ,解得
,解得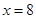 , 3分
, 3分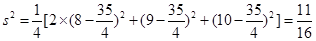 . 6分
. 6分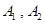 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.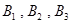 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.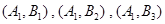 ,
, 共6种. 9分
共6种. 9分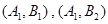 共2种.
共2种.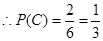 . 12分
. 12分

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
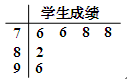
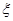 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求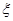 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
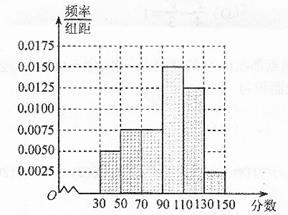
 ,求
,求 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
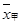 、
、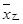 表示,则下列结论正确的是( )
表示,则下列结论正确的是( )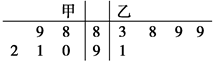
A.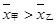 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定 | B.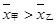 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定 |
C.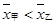 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定 | D.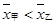 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 有责任 | 无责任 | 合计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1 200 |
| 合计 | 1 350 | 650 | 2 000 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
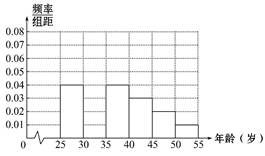
| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |

| P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
| 年龄组 是否低碳族 | 青 年 | 老 年 | 总 计 |
| 低碳族 | | | |
| 非低碳族 | | | |
| 总计 | | | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com