设函数f(x)=x-a(x+1)ln(x+1),(a≥0).
(1)如果a=1,求函数f(x)的单调递减区间;
(2)若函数f(x)在区间(-1,e-1)上单调递增,求实数a的取值范围;
(3)证明:当m>n>0时,(1+m)n<(1+n)m.
(1)解:函数f(x)的定义域为(-1,+∞)(1分)
f′(x)=1-aln(x+1)-a(2分)
当a=1时,f′(x)=-ln(x+1)
当x>0时,f′(x)<0.
所以f(x)的单调递减区间为(0,+∞).(4分)
(2)解:①当a=0时,f′(x)=1>0
∴f(x)在(-1,+∞)上是增函数 (5分)
②当a>0时,令
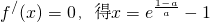
,
当f′(x)>0时,得
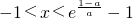
所以f(x)的递增区间为
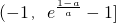
(7分)
又因为f(x)在区间(-1,e-1)上单调递增
所以
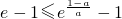
,由此得

(8分)
综上,得
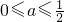
(9分)
(3)要证:(1+m)
n<(1+n)
m
只需证nln(1+m)<mln(1+n),
只需证
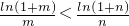
设
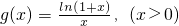
,(10分)
则
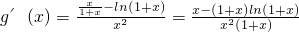
(11分)
由(1)知:即当a=1时,f(x)=x-(1+x)ln(1+x),在(0,+∞)单调递减,
即x>0时,有f(x)<f(0),-------(12分)
∴x-(1+x)ln(1+x)<0,所以g′(x)<0,
即g(x)是(0,+∞)上的减函数,(13分)
即当m>n>0时,g(m)<g(n),
故原不等式成立. (14分)
分析:(1)确定函数的定义域,求导函数,从而确定f(x)的单调递减区间;
(2)先确定函数的单调递增区间,再根据f(x)在区间(-1,e-1)上单调递增,建立不等式,从而可求实数a的取值范围;
(3)根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
点评:本题重点考查导数知识的运用,考查函数的单调性,考查不等式的证明,考查化归思想,考查构造函数,是一个综合题,解题时确定函数的单调性是关键.

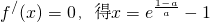 ,
,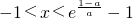
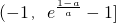 (7分)
(7分)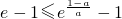 ,由此得
,由此得 (8分)
(8分)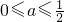 (9分)
(9分)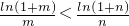
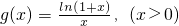 ,(10分)
,(10分)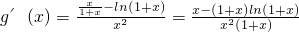 (11分)
(11分)
