
分析 由题意得$\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ,存在k∈Z,使φ=$\frac{π}{6}$+2kπ,由0<φ<$\frac{π}{2}$,求得φ的值.
解答 解:由题意可得f($\frac{π}{6}$)为f(x)的最大值为1,
即$\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ,k∈Z.
∴φ=$\frac{π}{6}$+2kπ,k∈Z.
∵0<φ<$\frac{π}{2}$,
∴k=0,φ=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题主要考查正弦函数的图象和性质,考查正弦函数的最值,以及运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
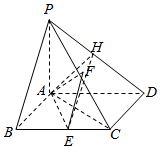 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在圆内接梯形ABCD中,AB∥CD.过点A作圆的切线与CB的延长线交于点E,若AB=AD=3,BE=2,
如图,在圆内接梯形ABCD中,AB∥CD.过点A作圆的切线与CB的延长线交于点E,若AB=AD=3,BE=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com