
【题目】已知函数f(x)=x3+ax2+bx+c在x![]() 与x=1时都取得极值,求a,b的值与函数f(x)的单调区间.
与x=1时都取得极值,求a,b的值与函数f(x)的单调区间.
【答案】a![]() ,b=﹣2,f(x)的递增区间是(﹣∞,
,b=﹣2,f(x)的递增区间是(﹣∞,![]() )和(1,+∞),递减区间是(
)和(1,+∞),递减区间是(![]() ,1).
,1).
【解析】
对f(x)求导,导函数在x![]() 与x=1函数值为0,求解a,b,分析导函数正负,从而得到函数f(x)的单调区间.
与x=1函数值为0,求解a,b,分析导函数正负,从而得到函数f(x)的单调区间.
解:(1)f(x)=x3+ax2+bx+c,f′(x)=3x2+2ax+b
由f′(![]() )
)![]() a+b=0,f′(1)=3+2a+b=0
a+b=0,f′(1)=3+2a+b=0
解得,a![]() ,b=﹣2.
,b=﹣2.
f′(x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
X | (﹣∞, |
| ( | 1 | (1,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以函数f(x)的递增区间是(﹣∞,![]() )和(1,+∞),递减区间是(
)和(1,+∞),递减区间是(![]() ,1).
,1).


科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海上进行工程建设时,一般需要在工地某处设置警戒水域;现有一海上作业工地记为点![]() ,在一个特定时段内,以点
,在一个特定时段内,以点![]() 为中心的1海里以内海域被设为警戒水域,点
为中心的1海里以内海域被设为警戒水域,点![]() 正北
正北![]() 海里处有一个雷达观测站
海里处有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距10海里的位置
相距10海里的位置![]() ,经过12分钟又测得该船已行驶到点
,经过12分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.试判断它是否会进入警戒水域(点![]() 与船的距离小于1海里即为进入警戒水域),并说明理由.
与船的距离小于1海里即为进入警戒水域),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代以六十年为一个甲子用十天干和十二地支相配六十年轮一遍,周而复始。甲子为干支之一,顺序为第一个前一位是癸亥,后一位是乙丑论阴阳五行,天干之甲属阳之木,地支之子属阳之水,是水生木相生,十干与十二支按顺序两两相配,从甲子到癸亥,共六十个组合,称六十甲子.
问题
(1)2020年是己亥年,至少多少年后又是己亥年?
(2)从一个已亥年到下一个己亥年,周期是多少?
(3)计算i,![]() ,
,![]() ,
,![]() ,…,一直计算下去,你会得到什么结论?
,…,一直计算下去,你会得到什么结论?
查看答案和解析>>
科目:高中数学 来源: 题型:
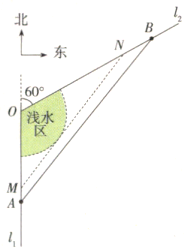
【题目】某港湾的平面示意图如图所示,![]() 、
、![]() 、
、![]() 分别是海岸线
分别是海岸线![]() 、
、![]() 上的三个集镇,
上的三个集镇,![]() 位于
位于![]() 的正南方向
的正南方向![]() 处,
处,![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向
方向![]() 处.随着经济的发展,为缓解集镇
处.随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 、
、![]() 上分别修建码头
上分别修建码头![]() 、
、![]() ,开辟水上航线,勘测时发现:以
,开辟水上航线,勘测时发现:以![]() 为圆心,
为圆心,![]() 为半径的扇形区域为浅水区,不适宜船只航行.
为半径的扇形区域为浅水区,不适宜船只航行.
(1)能否求出集镇![]() 、
、![]() 间的直线距离?
间的直线距离?
(2)根据勘测要求,要使![]() 、
、![]() 之间的直线航线最短,直线
之间的直线航线最短,直线![]() 与圆
与圆![]() 应满足什么关系?
应满足什么关系?
(3)应怎样确定码头![]() 、
、![]() 的位置,才能使得
的位置,才能使得![]() 、
、![]() 之间的直线航线最短?
之间的直线航线最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①所示的等边三角形![]() 的边长为
的边长为![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() 分别是
分别是![]() 边的中点现将
边的中点现将![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() ,如图②所示.
,如图②所示.


① ②
(1)试判断折叠后直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求四面体![]() 外接球的体积与四棱锥
外接球的体积与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com