
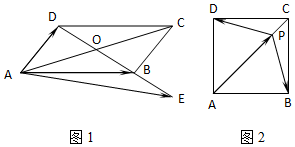
 (1)如图1,在平行四边形ABCD中,点E是对角线DB的延长线上一点,且OB=BE.记$\overrightarrow{AB}=\overrightarrow a\;,\;\overrightarrow{AD}=\overrightarrow b$,试用向量$\overrightarrow a\;,\;\overrightarrow b$表示$\overrightarrow{AE}$.
(1)如图1,在平行四边形ABCD中,点E是对角线DB的延长线上一点,且OB=BE.记$\overrightarrow{AB}=\overrightarrow a\;,\;\overrightarrow{AD}=\overrightarrow b$,试用向量$\overrightarrow a\;,\;\overrightarrow b$表示$\overrightarrow{AE}$.分析 (1)方法一:由向量的减法及加法运算,求得$\overrightarrow{AE}$=$\overrightarrow{AO}$+$\overrightarrow{OE}$,代入即可求得$\overrightarrow{AE}$;
方法二:利用加法的平行四边形法则,$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$),$\overrightarrow{AB}$=$\frac{1}{2}$($\overrightarrow{AO}$+$\overrightarrow{AE}$),则$\overrightarrow{AE}$=2$\overrightarrow{AB}$-$\overrightarrow{AO}$;
(2)建立直角坐标,根据向量的坐标表示,二次函数的性质,即可求得$\overrightarrow{AP}•(\overrightarrow{PB}+\overrightarrow{PD})$的取值范围;
(3)由||2+|$\overrightarrow{b}$|2=8,设||=2$\sqrt{2}$cosθ,|$\overrightarrow{b}$|=2$\sqrt{2}$sinθ;这样便可得出S△AOB=2sin2θsin∠AOB,从而sin2θ=1时△AOB的面积最大,这样由$\overrightarrow{a}$•$\overrightarrow{b}$=2即可得到cos∠AOB=$\frac{1}{2}$,从而便可得出∠AOB的大小.
解答 解:(1)由$\overrightarrow{DB}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$)=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),
由O为BD的中点,且OB=BE.则DB=OE,
∴$\overrightarrow{AE}$=$\overrightarrow{AO}$+$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$)+$\overrightarrow{a}$-$\overrightarrow{b}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{AE}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,.
方法二:由向量加法的平行四边形法则可知:$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$)=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),
由OB=BE.则$\overrightarrow{AB}$=$\frac{1}{2}$($\overrightarrow{AO}$+$\overrightarrow{AE}$),
则$\overrightarrow{AE}$=2$\overrightarrow{AB}$-$\overrightarrow{AO}$=2$\overrightarrow{a}$-$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{AE}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$.
(2)解:以AB,AC 为x,y轴建立直角坐标系则
A(0,0),B(1,0),C(1,1),D(0,1)
设P(x,x)(0≤x≤1),$\overrightarrow{AP}$=(x,x),$\overrightarrow{PD}$=(1-x,-x)
∴$\overrightarrow{AP}$=(-x,1-x),
$\overrightarrow{AP}•(\overrightarrow{PB}+\overrightarrow{PD})$=2x(1-2x)=-4(x-$\frac{1}{4}$)2+4(0≤x≤1)
∴当x=$\frac{1}{4}$时,函数有最大值$\frac{1}{4}$;当x=1时函数有最小值-2
∴$\overrightarrow{AP}•(\overrightarrow{PB}+\overrightarrow{PD})$的取值范围[-2,$\frac{1}{4}$],
(3)根据条件|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2-4+|$\overrightarrow{b}$|2=4;
∴||2+|$\overrightarrow{b}$|2=8;
∴设||=2$\sqrt{2}$cosθ,|$\overrightarrow{b}$|=2$\sqrt{2}$sinθ;
∴S△AOB=$\frac{1}{2}$|||$\overrightarrow{b}$|sin∠AOB=2sin2θsin∠AOB;
∴sin2θ=1时,△AOB的面积最大;
∴此时,$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$丨•丨$\overrightarrow{b}$|cos∠AOB=4sin2θcos∠AOB=4cos∠AOB=2;
∴cos∠AOB=$\frac{1}{2}$;
∴∠AOB=$\frac{π}{3}$,
∴∠AOB为$\frac{π}{3}$.
点评 本题考查向量的坐标运算,平面向量加法及减法运算,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-7)∪(1,+∞) | B. | (-∞,-7]∪[1,+∞) | C. | (-7,1) | D. | [-7,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $-\frac{{\sqrt{5}}}{5}$ | ||
| C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{-2xsinx-(1-{x^2})}}{sinx}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 纵坐标缩短为原来的$\frac{1}{2}$(横坐标不变),再向左平移1个单位 | |
| B. | 纵坐标缩短为原来的$\frac{1}{2}$(横坐标不变),再向左平移$\frac{1}{3}$个单位 | |
| C. | 横坐标伸长为原来的$\sqrt{2}$倍(纵坐标不变),再向左平移$\frac{1}{3}$个单位 | |
| D. | 横坐标伸长为原来的2倍(纵坐标不变),再向右平移1个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com