
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
【答案】
(1)证明:∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,
∴MN2=PN2=NANB,
∴ ![]() =
= ![]() ,
,
又∵∠PNA=∠BNP,
∴△PNA∽△BNP,
∴∠APN=∠PBN,即∠APM=∠PBA,.
∵MC=BC,
∴∠MAC=∠BAC,
∴∠MAP=∠PAB,
∴△APM∽△ABP
(2)证明:∵∠ACD=∠PBN,
∴∠ACD=∠PBN=∠APN,即∠PCD=∠CPM,
∴PM∥CD.
∵△APM∽△ABP,
∴∠PMA=∠BPA
∵PM是圆O的切线,
∴∠PMA=∠MCP,
∴∠PMA=∠BPA=∠MCP,即∠MCP=∠DPC,
∴MC∥PD,
∴四边形PMCD是平行四边形
【解析】(1)由切割线定理,及N是PM的中点,可得PN2=NANB,进而 ![]() =
= ![]() ,结合∠PNA=∠BNP,可得△PNA∽△BNP,则∠APN=∠PBN,即∠APM=∠PBA;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(2)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.
,结合∠PNA=∠BNP,可得△PNA∽△BNP,则∠APN=∠PBN,即∠APM=∠PBA;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(2)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n﹣1+a2n<0”的条件.(填“充要条件、充分不必要条件、必要不充分条件、即不充分也不必要条件”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() ,那么我们称数列
,那么我们称数列![]() 为“
为“![]() —摆动数列”.
—摆动数列”.
(![]() )设
)设![]() ,
, ![]() ,
, ![]() ,判断数列
,判断数列![]() ,
, ![]() 是否为“
是否为“![]() —摆动数列”,并说明理由;
—摆动数列”,并说明理由;
(2)已知“![]() —摆动数列”
—摆动数列”![]() 满足:
满足: ![]() ,求常数
,求常数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①函数![]() 的图象与
的图象与![]() 的图象恰有
的图象恰有![]() 个公共点;
个公共点;
②函数![]() 有
有![]() 个零点;
个零点;
③若函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称,则函数
对称,则函数![]() 与
与![]() 的图象也关于直线
的图象也关于直线![]() 对称;
对称;
④函数![]() 的图象是由函数
的图象是由函数![]() 的图象水平向右平移一个单位后,将所得图象在
的图象水平向右平移一个单位后,将所得图象在![]() 轴右侧部分沿
轴右侧部分沿![]() 轴翻折到
轴翻折到![]() 轴左侧替代
轴左侧替代![]() 轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号)
轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 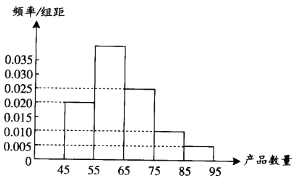
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]() ,x∈R.
,x∈R.
(1)求f(x)的单调递增区间;
(2)在锐角△ABC中,角A,B,C的对边分别a,b,c,若f(A)=![]() ,a=
,a=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com